Converting integers to larger integer types

We often need to sign extend a number into a larger type.  To keep the same value we sign extend. Unsigned numbers do not have a sign bit, so will be left padded with zeros.

The unsigned versions are pretty obvious:

void _mm_cvtepu32_epi64(const __m128i &mIn, __m128i &mOutLo, __m128i &mOutHi)
{
 mOutLo = _mm_unpacklo_epi32(mIn, _mm_setzero_si128());
 mOutHi = _mm_unpackhi_epi32(mIn, _mm_setzero_si128());
}
void _mm_cvtepu16_epi32(const __m128i &mIn, __m128i &mOutLo, __m128i &mOutHi)
{
 mOutLo = _mm_unpacklo_epi16(mIn, _mm_setzero_si128());
 mOutHi = _mm_unpackhi_epi16(mIn, _mm_setzero_si128());
}
void _mm_cvtepu8_epi16(const __m128i &mIn, __m128i &mOutLo, __m128i &mOutHi)
{
 mOutLo = _mm_unpacklo_epi8(mIn, _mm_setzero_si128());
 mOutHi = _mm_unpackhi_epi8(mIn, _mm_setzero_si128());
} 

The signed version aren't supported directly until later iterations of the instruction set with  _mm_cvtepi32_epi64 and other similar instructions, but it isn't too difficult produce from the base intrinsics.

void _mm_cvtepi16_epi32(const __m128i &mIn, __m128i &mOutLo, __m128i &mOutHi)
{
 __m128i mDupedLo = _mm_unpacklo_epi16(mIn, mIn);
 __m128i mDupedHi = _mm_unpackhi_epi16(mIn, mIn);
 mOutLo = _mm_srai_epi32(mDupedLo , 16);
 mOutHi = _mm_srai_epi32(mDupedHi , 16);
}
void _mm_cvtepi8_epi16(const __m128i &mIn, __m128i &mOutLo, __m128i &mOutHi)
{
 __m128i mDupedLo = _mm_unpacklo_epi8(mIn, mIn);
 __m128i mDupedHi = _mm_unpackhi_epi8(mIn, mIn);
 mOutLo = _mm_srai_epi16(mDupedLo , 8);
 mOutHi = _mm_srai_epi16(mDupedHi , 8);
}

But since there isn't a 64bit arithmetic shift, we need to do something different for the promotion from 32bit signed to 64 bit signed.  We extend the sign bit from each of the 4 lanes to all 32 bits of the lane.

Then we interleave the 32 bit results from the signs and values into the final 64 bit outputs.

void _mm_cvtepi32_epi64(const __m128i &mIn, __m128i &mOutLo, __m128i &mOutHi)
{
 __m128i mSigns = _mm_srai_epi32(mIn, 31);
 mOutLo = _mm_unpacklo_epi32(mIn, mSigns);
 mOutHi = _mm_unpackhi_epi32(mIn, mSigns);
}

This requires 3 registers rather than the 2 registers of the other width version.

number of leading zeroes in SSE2

The number of leading zeroes is often useful when doing division-like operations.  It's also particularly useful when each bit has been used to represent some sort of condition (similar to what was seen in the strlen post). 

The usefulness of this was formalized in the instruction set with _mm_lzcnt_epi32 and _lzcnt_u32.  But the __m128i processor instruction requires that the processor supports both AVX512VL + AVX512CD, and I don't own one of those computers yet.  The bitscan instructions have been available for over a decade, but don't handle __m128i

Here's a baseline implementation and an intrinsic instruction implementation.

unsigned nlz_baseline(unsigned x)
{
    unsigned uRet = 32;
    while (x)
    {
        uRet--;
        x = x>>1;
    }
    return uRet;
}

unsigned long nlz_bsr(unsigned long mask)
{
    unsigned long index;
    if (_BitScanReverse(&index, mask))
    {
        return 31 - index;
    }
    return 32;
}

The book "Hacker's delight" has a branch free implementation that translates directly to SSE2.  The lack of a conversion operator between epu32 and single floats in the SSE2 instruction set makes many of the bit re-interpretation strategies not work.

unsigned nlz(unsigned x)
{
    int y, m, n;
    y = -(x >> 16);
    m = (y >> 16) & 16;
    n = 16 - m;
    x = x >> m;
    y = x - 0x100;
    m = (y >> 16) & 8;
    n = n + m;
    x = x << m;
    y = x - 0x1000;
    m = (y >> 16) & 4;
    n = n + m;
    x = x << m;
    y = x - 0x4000;
    m = (y >> 16) & 2;
    n = n + m;
    x = x << m;
    y = x >> 14;
    m = y&~(y >> 1);
    return n + 2 - m;
}

__m128i nlz_SSE2(const __m128i &xIn)
{
    __m128i y, m, n;
    y = _mm_sub_epi32(_mm_setzero_si128(),_mm_srli_epi32(xIn, 16));
    m = _mm_and_si128(_mm_set1_epi32(16), _mm_srai_epi32(y, 16));
    n = _mm_sub_epi32(_mm_set1_epi32(16),m);
    __m128i x = _mm_srlv_epi32(xIn, m);
    y = _mm_sub_epi32(x, _mm_set1_epi32(0x100));
    m = _mm_and_si128(_mm_srai_epi32(y, 16), _mm_set1_epi32(8));
    n = _mm_add_epi32(n, m);
    x = _mm_sllv_epi32(x, m);
    y = _mm_sub_epi32(x, _mm_set1_epi32(0x1000));
    m = _mm_and_si128(_mm_srai_epi32(y, 16), _mm_set1_epi32(4));
    n = _mm_add_epi32(n, m);
    x = _mm_sllv_epi32(x, m);
    y = _mm_sub_epi32(x, _mm_set1_epi32(0x4000));
    m = _mm_and_si128(_mm_srai_epi32(y, 16), _mm_set1_epi32(2));
    n = _mm_add_epi32(n, m);
    x = _mm_sllv_epi32(x, m);
    y = _mm_srli_epi32(x, 14);
    m = _mm_andnot_si128(_mm_srai_epi32(y, 1),y);
    __m128i mRet = _mm_sub_epi32(_mm_add_epi32(n, _mm_set1_epi32(2)),m);
   
    return mRet;
}

Since this is written only for 32 bit integer numbers, every possible 32bit number is confirmed against the baseline implementation.

Transposing a 16x16 bit matrix using SSE2 and AVX2.

Building on the 16x8 matrix transpose from a previous post, it's pretty easy to make a 16x16 matrix transpose.

void BitMatrixTranspose_16x16_SSE(const __m128i &aIn, const __m128i &bIn, __m128i & cOut, __m128i &dOut)
{

    __m128i mLeft = BitMatrixTranspose_16x8_SSE(aIn);
    __m128i mRight = BitMatrixTranspose_16x8_SSE(bIn);
    cOut = _mm_unpacklo_epi8(mLeft, mRight);
    dOut = _mm_unpackhi_epi8(mLeft, mRight);
}

Most new machines support AVX and AVX2 these days.

__m256i unpack8_AVX2(const __m256i&xIn)
{
    __m256i mRet = _mm256_unpacklo_epi8(xIn, _mm256_shuffle_epi32(xIn, _MM_SHUFFLE(3, 2, 3, 2)));
    return mRet;
}

__m256i repack8_AVX2(const __m256i&xIn)
{
    return unpack8_SSE(unpack8_SSE(unpack8_SSE(xIn)));
}

__m256i BitMatrixTranspose_8x8_AVX2(const __m256i &xIn)
{
    const __m256i c1 = _mm256_set1_epi64x(0xAA55AA55AA55AA55LL);
    const __m256i c2 = _mm256_set1_epi64x(0x00AA00AA00AA00AALL);
    const __m256i c3 = _mm256_set1_epi64x(0xCCCC3333CCCC3333LL);
    const __m256i c4 = _mm256_set1_epi64x(0x0000CCCC0000CCCCLL);
    const __m256i c5 = _mm256_set1_epi64x(0xF0F0F0F00F0F0F0FLL);
    const __m256i c6 = _mm256_set1_epi64x(0x00000000F0F0F0F0LL);

    const __m256i x1 = _mm256_or_si256(_mm256_and_si256(xIn, c1), _mm256_or_si256(_mm256_slli_epi64(_mm256_and_si256(xIn, c2), 7), _mm256_and_si256(_mm256_srli_epi64(xIn, 7), c2)));
    const __m256i x2 = _mm256_or_si256(_mm256_and_si256(x1, c3), _mm256_or_si256(_mm256_slli_epi64(_mm256_and_si256(x1, c4), 14), _mm256_and_si256(_mm256_srli_epi64(x1, 14), c4)));
    const __m256i x3 = _mm256_or_si256(_mm256_and_si256(x2, c5), _mm256_or_si256(_mm256_slli_epi64(_mm256_and_si256(x2, c6), 28), _mm256_and_si256(_mm256_srli_epi64(x2, 28), c6)));

    return x3;
}

__m256i BitMatrixTranspose_16x16_AVX2(const __m256i &xIn)
{
    __m256i mUnshuffle = repack8_AVX2(xIn);
    __m256i mSmallTranspose= BitMatrixTranspose_8x8_AVX2(mUnshuffle);
    __m256i mRet = unpack8_across_lanes_AVX2(mSmallTranspose);
    return mRet;
}

This follows the same shuffle pattern used in SSE2.  But the shuffle could be rewritten and simplified using the arbitrary byte shuffle instruction:

__m256i repack8_AVX2(const __m256i&xIn)
{
    const __m256i xShuffleConst = _mm256_set_epi64x(0x0f0d0b0907050301LL, 0x0e0c0a0806040200LL, 0x0f0d0b0907050301LL, 0x0e0c0a0806040200LL);
    __m256i mRet = _mm256_shuffle_epi8(xIn, xShuffleConst);
    return mRet;
}

I would normally declare the above 256bit constant static.  But it appears that MSVC doesn't handle static __m256i variables as well as it does static __m128i.

Transposing a bit matrix using SSE2

In order to make a error correcting code more resilient to burst errors, it's not uncommon to interleave bits from multiple encoded words.  

Intuitively we can think of making a 2d matrix with each row being a separate codeword.  Interleaving the bits is then just taking the transpose of the bit matrix.

The book "Hacker's Delight" has an ansi algorithm for transposing a 8x8 bit matrix (64 bits total):

unsigned __int64 transpose8(unsigned __int64 x)
{
    x = (x & 0xAA55AA55AA55AA55LL) | ((x & 0x00AA00AA00AA00AALL) << 7) | ((x >> 7) & 0x00AA00AA00AA00AALL);
    x = (x & 0xCCCC3333CCCC3333LL) | ((x & 0x0000CCCC0000CCCCLL) << 14) | ((x >> 14) & 0x0000CCCC0000CCCCLL);
    x = (x & 0xF0F0F0F00F0F0F0FLL) | ((x & 0x00000000F0F0F0F0LL) << 28) | ((x >> 28) & 0x00000000F0F0F0F0LL);
    return x;
}

This can be directly translated into SSE code, which will transpose two separate 8x8 matrices at the same time:

__m128i BitMatrixTranspose_8x8_SSE(const __m128i &xIn)
{
    const __m128i c1 = _mm_set1_epi64x(0xAA55AA55AA55AA55LL);
    const __m128i c2 = _mm_set1_epi64x(0x00AA00AA00AA00AALL);
    const __m128i c3 = _mm_set1_epi64x(0xCCCC3333CCCC3333LL);
    const __m128i c4 = _mm_set1_epi64x(0x0000CCCC0000CCCCLL);
    const __m128i c5 = _mm_set1_epi64x(0xF0F0F0F00F0F0F0FLL);
    const __m128i c6 = _mm_set1_epi64x(0x00000000F0F0F0F0LL);

    const __m128i x1 = _mm_or_si128(_mm_and_si128(xIn, c1), _mm_or_si128(_mm_slli_epi64(_mm_and_si128(xIn, c2), 7), _mm_and_si128(_mm_srli_epi64(xIn, 7), c2)));
    const __m128i x2 = _mm_or_si128(_mm_and_si128(x1, c3), _mm_or_si128(_mm_slli_epi64(_mm_and_si128(x1, c4), 14), _mm_and_si128(_mm_srli_epi64(x1, 14), c4)));
    const __m128i x3 = _mm_or_si128(_mm_and_si128(x2, c5), _mm_or_si128(_mm_slli_epi64(_mm_and_si128(x2, c6), 28), _mm_and_si128(_mm_srli_epi64(x2, 28), c6)));

    return x3;
}

A transpose operation on a square matrix is self inverse.  So the above function is self inverse.

This can then be extended to take the transpose of an 8x16 matrix and a 16x8 matrix (inverse functions of each other).

__m128i unpack8_SSE(const __m128i&xIn)
{
    __m128i mRet = _mm_unpacklo_epi8(xIn, _mm_shuffle_epi32(xIn, _MM_SHUFFLE(3, 2, 3, 2)));
    return mRet;
}

__m128i repack8_SSE(const __m128i&xIn)
{
    return unpack8_SSE(unpack8_SSE(unpack8_SSE(xIn)));
}

__m128i BitMatrixTranspose_8x16_SSE(const __m128i &xIn)
{
    __m128i mTransposedHalves = BitMatrixTranspose_8x8_SSE(xIn);
    __m128i mRet = unpack8_SSE(mTransposedHalves);
    return mRet;
}

__m128i BitMatrixTranspose_16x8_SSE(const __m128i &xIn)
{
    __m128i mUnshuffle = repack8_SSE(xIn);
    __m128i mRet = BitMatrixTranspose_8x8_SSE(mUnshuffle);
    return mRet;
}

It's also worth noting that unpack8_SSE and repack8_SSE are inverses of each other.
This could be simplified using the _mm_shuffle_epi8 instruction.  But that's a different problem.

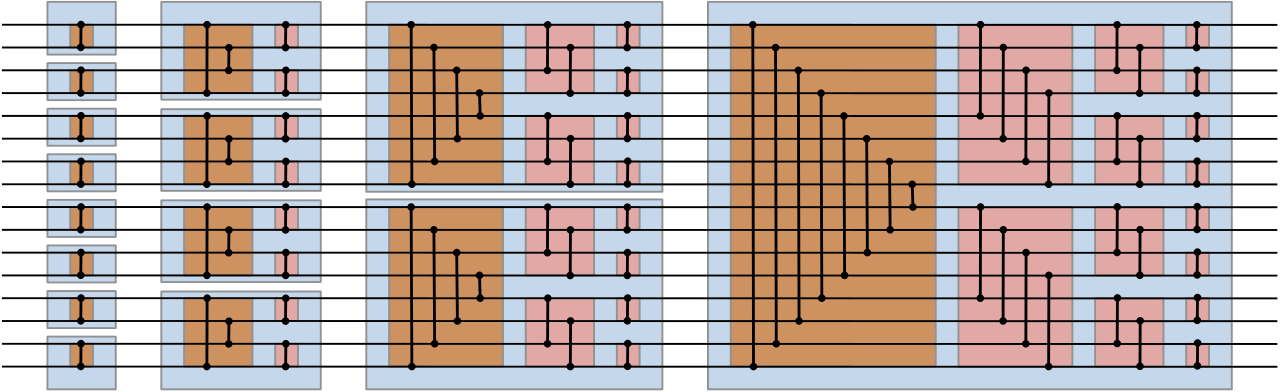
A bitonic sorting network for 16 float in SSE2

A while back I gave source code for a 8 float bitonic sorting network.
Bitonic sorting networks can be recursively expanded to larger sorting networks.  So we have the main building block for a 16 float bitonic sorting network.  The two halves are sorted, then merged together.

Here's the previously seen 8 float network.

void BitonicSortingNetwork8_SSE2(const __m128 &a, const __m128 &b, __m128 &aOut, __m128 &bOut)
{
    __m128 a1 = a;
    __m128 b1 = b;
    __m128 a1Min = _mm_min_ps(a1, b1); // 1357
    __m128 b1Max = _mm_max_ps(a1, b1); // 2468
    __m128 a2 = a1Min; // 1357
    __m128 b2 = _mm_shuffle_ps(b1Max, b1Max, _MM_SHUFFLE(2, 3, 0, 1)); // 4286
    __m128 a2Min = _mm_min_ps(a2, b2); // 1256
    __m128 b2Max = _mm_max_ps(a2, b2); // 4387
    __m128 a3 = _mm_shuffle_ps(a2Min, b2Max, _MM_SHUFFLE(3, 1, 2, 0)); // 1537
    __m128 b3 = _mm_shuffle_ps(a2Min, b2Max, _MM_SHUFFLE(2, 0, 3, 1)); // 2648
    __m128 a3Min = _mm_min_ps(a3, b3); // 1537
    __m128 b3Max = _mm_max_ps(a3, b3); // 2648
    __m128 a4 = a3Min; // 1537
    __m128 b4 = _mm_shuffle_ps(b3Max, b3Max, _MM_SHUFFLE(0, 1, 2, 3)); // 8462
    __m128 a4Min = _mm_min_ps(a4, b4); // 1432
    __m128 b4Max = _mm_max_ps(a4, b4); // 8567
    __m128 a5 = _mm_unpacklo_ps(a4Min, b4Max); // 1845
    __m128 b5 = _mm_unpackhi_ps(a4Min, b4Max); // 3627
    __m128 a5Min = _mm_min_ps(a5, b5); // 1625
    __m128 b5Max = _mm_max_ps(a5, b5); // 3847
    __m128 a6 = _mm_unpacklo_ps(a5Min, b5Max); // 1368
    __m128 b6 = _mm_unpackhi_ps(a5Min, b5Max); // 2457
    __m128 a6Min = _mm_min_ps(a6, b6); // 1357
    __m128 b6Max = _mm_max_ps(a6, b6); // 2468
    aOut = _mm_unpacklo_ps(a6Min, b6Max); // 1234
    bOut = _mm_unpackhi_ps(a6Min, b6Max); // 5678
}

This is the topLeft group of the 16 float network.  It is also the bottomLeft group of the 16 float network.

This leaves the right half.  The last 3 sets of comparisons look like the last 3 comparisons of the 8 float network.

void UpperHalfRightHalfBitonicSorter_SSE2(const __m128 &aIn, const __m128 &bIn, __m128 &aOut, __m128 &bOut)
{
    __m128 a1 = aIn; // 1234
    __m128 b1 = bIn; // 5678
    __m128 a1Min = _mm_min_ps(a1, b1); // 1234
    __m128 b1Max = _mm_max_ps(a1, b1); // 5678
    __m128 a2 = _mm_unpacklo_ps(a1Min, b1Max); // 1526
    __m128 b2 = _mm_unpackhi_ps(a1Min, b1Max); // 3748
    __m128 a2Min = _mm_min_ps(a2, b2); // 1526
    __m128 b2Max = _mm_max_ps(a2, b2); // 3748
    __m128 a3 = _mm_unpacklo_ps(a2Min, b2Max); // 1357
    __m128 b3 = _mm_unpackhi_ps(a2Min, b2Max); // 2468
    __m128 a3Min = _mm_min_ps(a3, b3); // 1357
    __m128 b3Max = _mm_max_ps(a3, b3); // 2468
    aOut = _mm_unpacklo_ps(a3Min, b3Max); // 1234
    bOut = _mm_unpackhi_ps(a3Min, b3Max); // 5678
}

And then there's the large group of 16 comparisons in the very center.
And it all gets put together.

void BitonicSortingNetwork16_SSE2(const __m128 &aIn, const __m128 &bIn, const __m128 &cIn, const __m128 &dIn,

    __m128 &aOut, __m128 &bOut, __m128 &cOut, __m128 &dOut

)

{

    __m128 a1 = aIn, b1 = bIn, c1 = cIn, d1 = dIn;

    __m128 a2, b2, c2, d2;

    BitonicSortingNetwork8_SSE2(a1, b1, a2, b2);

    BitonicSortingNetwork8_SSE2(c1, d1, c2, d2);

    __m128 a3 = a2, b3 = b2;

    __m128 c3 = _mm_shuffle_ps(c2, c2, _MM_SHUFFLE(0, 1, 2, 3));

    __m128 d3 = _mm_shuffle_ps(d2, d2, _MM_SHUFFLE(0, 1, 2, 3));

    __m128 ad3Min = _mm_min_ps(a3, d3);

    __m128 ad3Max = _mm_max_ps(a3, d3);

    __m128 bc3Min = _mm_min_ps(b3, c3);

    __m128 bc3Max = _mm_max_ps(b3, c3);

    __m128 a4 = ad3Min;
    __m128 b4 = bc3Min;
    __m128 c4 = _mm_shuffle_ps(bc3Max, bc3Max, _MM_SHUFFLE(0, 1, 2, 3));
    __m128 d4 = _mm_shuffle_ps(ad3Max, ad3Max, _MM_SHUFFLE(0, 1, 2, 3));
    UpperHalfRightHalfBitonicSorter_SSE2(a4, b4, aOut, bOut);
    UpperHalfRightHalfBitonicSorter_SSE2(c4, d4, cOut, dOut);

}

This is verified using the 0/1 method described in Knuth.

Reversing the 16bit numbers in an XMM register using SSE2 and SSSE3

A bunch of algorithms end up requiring reversing the order of a bunch of bytes.  In particular I've seen this come up a lot in code to decompress GIF images. A diagonal string distance algorithm on standard char strings would require reversing a string of bytes.

But my world doesn't involve many single width strings.  My world tends to have 16bit Unicode strings.  So reversing a string of 16bit characters will instead come up.  16bit numbers are treated the same as 16bit Unicode characters.

This can be done just with SSE2 instructions.

__m128i _mm_reverse_epi16_SSE2(const __m128i &mToReverse)
{
    __m128i mReversed_epi32 = _mm_shuffle_epi32(mToReverse, _MM_SHUFFLE(0, 1, 2, 3));
    __m128i mLowDone = _mm_shufflelo_epi16(mReversed_epi32, _MM_SHUFFLE(2, 3, 0, 1));
    __m128i mResult = _mm_shufflehi_epi16(mLowDone, _MM_SHUFFLE(2, 3, 0, 1));
    return mResult;
}

But in fact can be done in a single instruction in SSSE3 (since the pshufb instruction supports using a  memory address for the second parameter).

__m128i _mm_reverse_epi16_SSSE3(const __m128i &mToReverse)
{
    static const __m128i reverseKeys = { 14,15,12,13,10,11,8,9,6,7,4,5,2,3,0,1 };
    __m128i mResult = _mm_shuffle_epi8(mToReverse, reverseKeys);
    return mResult;
}

This is satisfying.

Levenshtein distance calculated on the diagonal (but only in ANSI for now)

A long time ago I promised to talk about a better way of calculating Levenshtein distance (edit distance).  A way that is more conducive to vectorization.
The trick is to calculate the same edit distance matrix as the standard two row method, but instead fill in the values in a diagonal manner.
This ends up having each diagonal depending on the previous two diagonals.  But importantly each diagonal does not depend on any other element of itself.

size_t Levenshtein_distance_diagonal_ANSI(const wchar_t* const s, const wchar_t* const t)
{
    const unsigned int lenS = wcslen(s);
    const unsigned int lenT = wcslen(t);
    if (0 == lenS)
    {
        return lenT;
    }
    if (0 == lenT)
    {
        return lenS;
    }
    if (0 == wcscmp(s, t))
    {
        return 0;
    }

    // create work vectors of integer distances
    unsigned int *v0 = new unsigned int[lenT + 1];
    unsigned int *v1 = new unsigned int[lenT + 1];
    unsigned int *v2 = new unsigned int[lenT + 1];

    v1[0] = 0;
    for (unsigned int j =1; j <= (lenS+lenT); j++)
    {
        unsigned int iMin;
        unsigned int iMax;
        v2[0] = j * 1;
        iMin = (unsigned int)max(1, (int)(j - lenS));
        if (j <= lenT)
        {
            v2[j] = j * 1;
            iMax = j-1;
        }
        else
        {
            iMax = lenT;
        }

        for (unsigned int i = iMin; i <= iMax; i++)
        {
            unsigned int substituteCost = v0[i-1]+(s[j-i-1] != t[i-1]);
            unsigned int insertionCost = v1[i-1]+1;
            unsigned int deletionCost = v1[i]+1;
            v2[i] = min(min(substituteCost, insertionCost), deletionCost);
        }
        unsigned int * const vTemp = v0;
        v0 = v1;
        v1 = v2;
        v2 = vTemp;
    }

    unsigned int retVal = v1[lenT];
    delete[] v0;
    delete[] v1;
    delete[] v2;
    return retVal;
}

While this implementation is not any better than the two row implementation, we can see where this is going.
This also can work with storage only for two diagonals, overwriting a diagonal just after its value is read.