A bitonic sorting network for 16 float in SSE2

A while back I gave source code for a 8 float bitonic sorting network.
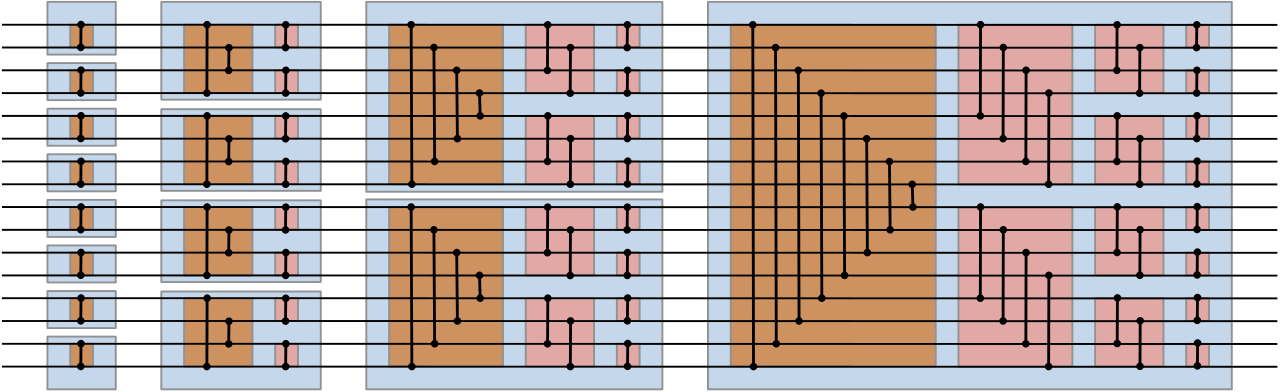
Bitonic sorting networks can be recursively expanded to larger sorting networks.  So we have the main building block for a 16 float bitonic sorting network.  The two halves are sorted, then merged together.

Here's the previously seen 8 float network.

void BitonicSortingNetwork8_SSE2(const __m128 &a, const __m128 &b, __m128 &aOut, __m128 &bOut)
{
    __m128 a1 = a;
    __m128 b1 = b;
    __m128 a1Min = _mm_min_ps(a1, b1); // 1357
    __m128 b1Max = _mm_max_ps(a1, b1); // 2468
    __m128 a2 = a1Min; // 1357
    __m128 b2 = _mm_shuffle_ps(b1Max, b1Max, _MM_SHUFFLE(2, 3, 0, 1)); // 4286
    __m128 a2Min = _mm_min_ps(a2, b2); // 1256
    __m128 b2Max = _mm_max_ps(a2, b2); // 4387
    __m128 a3 = _mm_shuffle_ps(a2Min, b2Max, _MM_SHUFFLE(3, 1, 2, 0)); // 1537
    __m128 b3 = _mm_shuffle_ps(a2Min, b2Max, _MM_SHUFFLE(2, 0, 3, 1)); // 2648
    __m128 a3Min = _mm_min_ps(a3, b3); // 1537
    __m128 b3Max = _mm_max_ps(a3, b3); // 2648
    __m128 a4 = a3Min; // 1537
    __m128 b4 = _mm_shuffle_ps(b3Max, b3Max, _MM_SHUFFLE(0, 1, 2, 3)); // 8462
    __m128 a4Min = _mm_min_ps(a4, b4); // 1432
    __m128 b4Max = _mm_max_ps(a4, b4); // 8567
    __m128 a5 = _mm_unpacklo_ps(a4Min, b4Max); // 1845
    __m128 b5 = _mm_unpackhi_ps(a4Min, b4Max); // 3627
    __m128 a5Min = _mm_min_ps(a5, b5); // 1625
    __m128 b5Max = _mm_max_ps(a5, b5); // 3847
    __m128 a6 = _mm_unpacklo_ps(a5Min, b5Max); // 1368
    __m128 b6 = _mm_unpackhi_ps(a5Min, b5Max); // 2457
    __m128 a6Min = _mm_min_ps(a6, b6); // 1357
    __m128 b6Max = _mm_max_ps(a6, b6); // 2468
    aOut = _mm_unpacklo_ps(a6Min, b6Max); // 1234
    bOut = _mm_unpackhi_ps(a6Min, b6Max); // 5678
}

This is the topLeft group of the 16 float network.  It is also the bottomLeft group of the 16 float network.

This leaves the right half.  The last 3 sets of comparisons look like the last 3 comparisons of the 8 float network.

void UpperHalfRightHalfBitonicSorter_SSE2(const __m128 &aIn, const __m128 &bIn, __m128 &aOut, __m128 &bOut)
{
    __m128 a1 = aIn; // 1234
    __m128 b1 = bIn; // 5678
    __m128 a1Min = _mm_min_ps(a1, b1); // 1234
    __m128 b1Max = _mm_max_ps(a1, b1); // 5678
    __m128 a2 = _mm_unpacklo_ps(a1Min, b1Max); // 1526
    __m128 b2 = _mm_unpackhi_ps(a1Min, b1Max); // 3748
    __m128 a2Min = _mm_min_ps(a2, b2); // 1526
    __m128 b2Max = _mm_max_ps(a2, b2); // 3748
    __m128 a3 = _mm_unpacklo_ps(a2Min, b2Max); // 1357
    __m128 b3 = _mm_unpackhi_ps(a2Min, b2Max); // 2468
    __m128 a3Min = _mm_min_ps(a3, b3); // 1357
    __m128 b3Max = _mm_max_ps(a3, b3); // 2468
    aOut = _mm_unpacklo_ps(a3Min, b3Max); // 1234
    bOut = _mm_unpackhi_ps(a3Min, b3Max); // 5678
}

And then there's the large group of 16 comparisons in the very center.
And it all gets put together.

void BitonicSortingNetwork16_SSE2(const __m128 &aIn, const __m128 &bIn, const __m128 &cIn, const __m128 &dIn,

    __m128 &aOut, __m128 &bOut, __m128 &cOut, __m128 &dOut

)

{

    __m128 a1 = aIn, b1 = bIn, c1 = cIn, d1 = dIn;

    __m128 a2, b2, c2, d2;

    BitonicSortingNetwork8_SSE2(a1, b1, a2, b2);

    BitonicSortingNetwork8_SSE2(c1, d1, c2, d2);

    __m128 a3 = a2, b3 = b2;

    __m128 c3 = _mm_shuffle_ps(c2, c2, _MM_SHUFFLE(0, 1, 2, 3));

    __m128 d3 = _mm_shuffle_ps(d2, d2, _MM_SHUFFLE(0, 1, 2, 3));

    __m128 ad3Min = _mm_min_ps(a3, d3);

    __m128 ad3Max = _mm_max_ps(a3, d3);

    __m128 bc3Min = _mm_min_ps(b3, c3);

    __m128 bc3Max = _mm_max_ps(b3, c3);

    __m128 a4 = ad3Min;
    __m128 b4 = bc3Min;
    __m128 c4 = _mm_shuffle_ps(bc3Max, bc3Max, _MM_SHUFFLE(0, 1, 2, 3));
    __m128 d4 = _mm_shuffle_ps(ad3Max, ad3Max, _MM_SHUFFLE(0, 1, 2, 3));
    UpperHalfRightHalfBitonicSorter_SSE2(a4, b4, aOut, bOut);
    UpperHalfRightHalfBitonicSorter_SSE2(c4, d4, cOut, dOut);

}

This is verified using the 0/1 method described in Knuth.