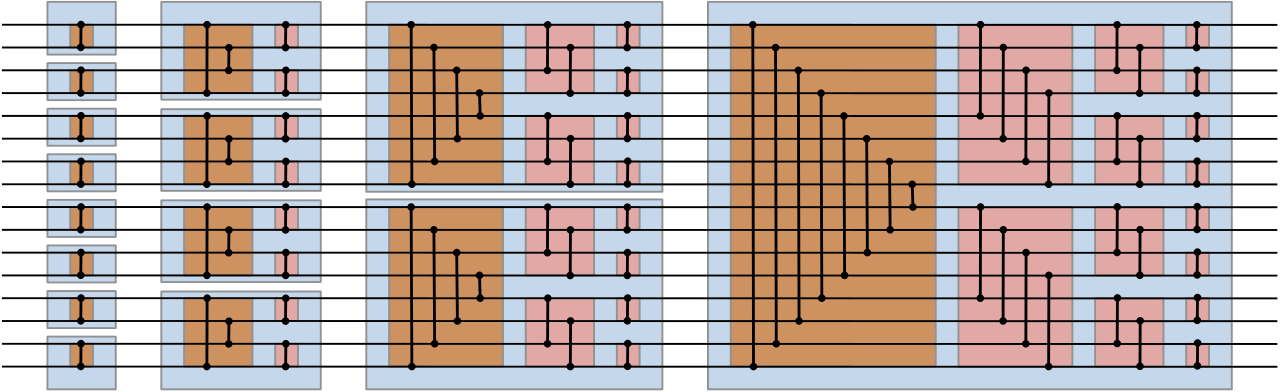
We often need to sign extend a number into a larger type. To keep the same value we sign extend. Unsigned numbers do not have a sign bit, so will be left padded with zeros.
The unsigned versions are pretty obvious:
void _mm_cvtepu32_epi64(const __m128i &mIn, __m128i &mOutLo, __m128i &mOutHi)
{
mOutLo = _mm_unpacklo_epi32(mIn, _mm_setzero_si128());
mOutHi = _mm_unpackhi_epi32(mIn, _mm_setzero_si128());
}
void _mm_cvtepu16_epi32(const __m128i &mIn, __m128i &mOutLo, __m128i &mOutHi)
{
mOutLo = _mm_unpacklo_epi16(mIn, _mm_setzero_si128());
mOutHi = _mm_unpackhi_epi16(mIn, _mm_setzero_si128());
}
void _mm_cvtepu8_epi16(const __m128i &mIn, __m128i &mOutLo, __m128i &mOutHi)
{
mOutLo = _mm_unpacklo_epi8(mIn, _mm_setzero_si128());
mOutHi = _mm_unpackhi_epi8(mIn, _mm_setzero_si128());
}
The signed version aren't supported directly until later iterations of the instruction set with _mm_cvtepi32_epi64 and other similar instructions, but it isn't too difficult produce from the base intrinsics.
void _mm_cvtepi16_epi32(const __m128i &mIn, __m128i &mOutLo, __m128i &mOutHi)
{
__m128i mDupedLo = _mm_unpacklo_epi16(mIn, mIn);
__m128i mDupedHi = _mm_unpackhi_epi16(mIn, mIn);
mOutLo = _mm_srai_epi32(mDupedLo , 16);
mOutHi = _mm_srai_epi32(mDupedHi , 16);
}
void _mm_cvtepi8_epi16(const __m128i &mIn, __m128i &mOutLo, __m128i &mOutHi)
{
__m128i mDupedLo = _mm_unpacklo_epi8(mIn, mIn);
__m128i mDupedHi = _mm_unpackhi_epi8(mIn, mIn);
mOutLo = _mm_srai_epi16(mDupedLo , 8);
mOutHi = _mm_srai_epi16(mDupedHi , 8);
}
But since there isn't a 64bit arithmetic shift, we need to do something different for the promotion from 32bit signed to 64 bit signed. We extend the sign bit from each of the 4 lanes to all 32 bits of the lane.
Then we interleave the 32 bit results from the signs and values into the final 64 bit outputs.
void _mm_cvtepi32_epi64(const __m128i &mIn, __m128i &mOutLo, __m128i &mOutHi)
{
__m128i mSigns = _mm_srai_epi32(mIn, 31);
mOutLo = _mm_unpacklo_epi32(mIn, mSigns);
mOutHi = _mm_unpackhi_epi32(mIn, mSigns);
}
This requires 3 registers rather than the 2 registers of the other width version.
Wednesday, December 20, 2017
Saturday, November 4, 2017
number of leading zeroes in SSE2
The number of leading zeroes is often useful when doing division-like operations. It's also particularly useful when each bit has been used to represent some sort of condition (similar to what was seen in the strlen post).
The usefulness of this was formalized in the instruction set with _mm_lzcnt_epi32 and _lzcnt_u32. But the __m128i processor instruction requires that the processor supports both AVX512VL + AVX512CD, and I don't own one of those computers yet. The bitscan instructions have been available for over a decade, but don't handle __m128i
Here's a baseline implementation and an intrinsic instruction implementation.
unsigned nlz_baseline(unsigned x)
{
unsigned uRet = 32;
while (x)
{
uRet--;
x = x>>1;
}
return uRet;
}
unsigned long nlz_bsr(unsigned long mask)
{
unsigned long index;
if (_BitScanReverse(&index, mask))
{
return 31 - index;
}
return 32;
}
The book "Hacker's delight" has a branch free implementation that translates directly to SSE2. The lack of a conversion operator between epu32 and single floats in the SSE2 instruction set makes many of the bit re-interpretation strategies not work.
unsigned nlz(unsigned x)
{
int y, m, n;
y = -(x >> 16);
m = (y >> 16) & 16;
n = 16 - m;
x = x >> m;
y = x - 0x100;
m = (y >> 16) & 8;
n = n + m;
x = x << m;
y = x - 0x1000;
m = (y >> 16) & 4;
n = n + m;
x = x << m;
y = x - 0x4000;
m = (y >> 16) & 2;
n = n + m;
x = x << m;
y = x >> 14;
m = y&~(y >> 1);
return n + 2 - m;
}
__m128i nlz_SSE2(const __m128i &xIn)
{
__m128i y, m, n;
y = _mm_sub_epi32(_mm_setzero_si128(),_mm_srli_epi32(xIn, 16));
m = _mm_and_si128(_mm_set1_epi32(16), _mm_srai_epi32(y, 16));
n = _mm_sub_epi32(_mm_set1_epi32(16),m);
__m128i x = _mm_srlv_epi32(xIn, m);
y = _mm_sub_epi32(x, _mm_set1_epi32(0x100));
m = _mm_and_si128(_mm_srai_epi32(y, 16), _mm_set1_epi32(8));
n = _mm_add_epi32(n, m);
x = _mm_sllv_epi32(x, m);
y = _mm_sub_epi32(x, _mm_set1_epi32(0x1000));
m = _mm_and_si128(_mm_srai_epi32(y, 16), _mm_set1_epi32(4));
n = _mm_add_epi32(n, m);
x = _mm_sllv_epi32(x, m);
y = _mm_sub_epi32(x, _mm_set1_epi32(0x4000));
m = _mm_and_si128(_mm_srai_epi32(y, 16), _mm_set1_epi32(2));
n = _mm_add_epi32(n, m);
x = _mm_sllv_epi32(x, m);
y = _mm_srli_epi32(x, 14);
m = _mm_andnot_si128(_mm_srai_epi32(y, 1),y);
__m128i mRet = _mm_sub_epi32(_mm_add_epi32(n, _mm_set1_epi32(2)),m);
return mRet;
}
Since this is written only for 32 bit integer numbers, every possible 32bit number is confirmed against the baseline implementation.
The usefulness of this was formalized in the instruction set with _mm_lzcnt_epi32 and _lzcnt_u32. But the __m128i processor instruction requires that the processor supports both AVX512VL + AVX512CD, and I don't own one of those computers yet. The bitscan instructions have been available for over a decade, but don't handle __m128i
Here's a baseline implementation and an intrinsic instruction implementation.
unsigned nlz_baseline(unsigned x)
{
unsigned uRet = 32;
while (x)
{
uRet--;
x = x>>1;
}
return uRet;
}
unsigned long nlz_bsr(unsigned long mask)
{
unsigned long index;
if (_BitScanReverse(&index, mask))
{
return 31 - index;
}
return 32;
}
The book "Hacker's delight" has a branch free implementation that translates directly to SSE2. The lack of a conversion operator between epu32 and single floats in the SSE2 instruction set makes many of the bit re-interpretation strategies not work.
unsigned nlz(unsigned x)
{
int y, m, n;
y = -(x >> 16);
m = (y >> 16) & 16;
n = 16 - m;
x = x >> m;
y = x - 0x100;
m = (y >> 16) & 8;
n = n + m;
x = x << m;
y = x - 0x1000;
m = (y >> 16) & 4;
n = n + m;
x = x << m;
y = x - 0x4000;
m = (y >> 16) & 2;
n = n + m;
x = x << m;
y = x >> 14;
m = y&~(y >> 1);
return n + 2 - m;
}
__m128i nlz_SSE2(const __m128i &xIn)
{
__m128i y, m, n;
y = _mm_sub_epi32(_mm_setzero_si128(),_mm_srli_epi32(xIn, 16));
m = _mm_and_si128(_mm_set1_epi32(16), _mm_srai_epi32(y, 16));
n = _mm_sub_epi32(_mm_set1_epi32(16),m);
__m128i x = _mm_srlv_epi32(xIn, m);
y = _mm_sub_epi32(x, _mm_set1_epi32(0x100));
m = _mm_and_si128(_mm_srai_epi32(y, 16), _mm_set1_epi32(8));
n = _mm_add_epi32(n, m);
x = _mm_sllv_epi32(x, m);
y = _mm_sub_epi32(x, _mm_set1_epi32(0x1000));
m = _mm_and_si128(_mm_srai_epi32(y, 16), _mm_set1_epi32(4));
n = _mm_add_epi32(n, m);
x = _mm_sllv_epi32(x, m);
y = _mm_sub_epi32(x, _mm_set1_epi32(0x4000));
m = _mm_and_si128(_mm_srai_epi32(y, 16), _mm_set1_epi32(2));
n = _mm_add_epi32(n, m);
x = _mm_sllv_epi32(x, m);
y = _mm_srli_epi32(x, 14);
m = _mm_andnot_si128(_mm_srai_epi32(y, 1),y);
__m128i mRet = _mm_sub_epi32(_mm_add_epi32(n, _mm_set1_epi32(2)),m);
return mRet;
}
Since this is written only for 32 bit integer numbers, every possible 32bit number is confirmed against the baseline implementation.
Sunday, October 29, 2017
Transposing a 16x16 bit matrix using SSE2 and AVX2.
Building on the 16x8 matrix transpose from a previous post, it's pretty easy to make a 16x16 matrix transpose.
void BitMatrixTranspose_16x16_SSE(const __m128i &aIn, const __m128i &bIn, __m128i & cOut, __m128i &dOut)
{
__m128i mLeft = BitMatrixTranspose_16x8_SSE(aIn);
__m128i mRight = BitMatrixTranspose_16x8_SSE(bIn);
cOut = _mm_unpacklo_epi8(mLeft, mRight);
dOut = _mm_unpackhi_epi8(mLeft, mRight);
}
Most new machines support AVX and AVX2 these days.
__m256i unpack8_AVX2(const __m256i&xIn)
{
__m256i mRet = _mm256_unpacklo_epi8(xIn, _mm256_shuffle_epi32(xIn, _MM_SHUFFLE(3, 2, 3, 2)));
return mRet;
}
__m256i repack8_AVX2(const __m256i&xIn)
{
return unpack8_SSE(unpack8_SSE(unpack8_SSE(xIn)));
}
__m256i BitMatrixTranspose_8x8_AVX2(const __m256i &xIn)
{
const __m256i c1 = _mm256_set1_epi64x(0xAA55AA55AA55AA55LL);
const __m256i c2 = _mm256_set1_epi64x(0x00AA00AA00AA00AALL);
const __m256i c3 = _mm256_set1_epi64x(0xCCCC3333CCCC3333LL);
const __m256i c4 = _mm256_set1_epi64x(0x0000CCCC0000CCCCLL);
const __m256i c5 = _mm256_set1_epi64x(0xF0F0F0F00F0F0F0FLL);
const __m256i c6 = _mm256_set1_epi64x(0x00000000F0F0F0F0LL);
const __m256i x1 = _mm256_or_si256(_mm256_and_si256(xIn, c1), _mm256_or_si256(_mm256_slli_epi64(_mm256_and_si256(xIn, c2), 7), _mm256_and_si256(_mm256_srli_epi64(xIn, 7), c2)));
const __m256i x2 = _mm256_or_si256(_mm256_and_si256(x1, c3), _mm256_or_si256(_mm256_slli_epi64(_mm256_and_si256(x1, c4), 14), _mm256_and_si256(_mm256_srli_epi64(x1, 14), c4)));
const __m256i x3 = _mm256_or_si256(_mm256_and_si256(x2, c5), _mm256_or_si256(_mm256_slli_epi64(_mm256_and_si256(x2, c6), 28), _mm256_and_si256(_mm256_srli_epi64(x2, 28), c6)));
return x3;
}
__m256i BitMatrixTranspose_16x16_AVX2(const __m256i &xIn)
{
__m256i mUnshuffle = repack8_AVX2(xIn);
__m256i mSmallTranspose= BitMatrixTranspose_8x8_AVX2(mUnshuffle);
__m256i mRet = unpack8_across_lanes_AVX2(mSmallTranspose);
return mRet;
}
This follows the same shuffle pattern used in SSE2. But the shuffle could be rewritten and simplified using the arbitrary byte shuffle instruction:
__m256i repack8_AVX2(const __m256i&xIn)
{
const __m256i xShuffleConst = _mm256_set_epi64x(0x0f0d0b0907050301LL, 0x0e0c0a0806040200LL, 0x0f0d0b0907050301LL, 0x0e0c0a0806040200LL);
__m256i mRet = _mm256_shuffle_epi8(xIn, xShuffleConst);
return mRet;
}
I would normally declare the above 256bit constant static. But it appears that MSVC doesn't handle static __m256i variables as well as it does static __m128i.
void BitMatrixTranspose_16x16_SSE(const __m128i &aIn, const __m128i &bIn, __m128i & cOut, __m128i &dOut)
{
__m128i mLeft = BitMatrixTranspose_16x8_SSE(aIn);
__m128i mRight = BitMatrixTranspose_16x8_SSE(bIn);
cOut = _mm_unpacklo_epi8(mLeft, mRight);
dOut = _mm_unpackhi_epi8(mLeft, mRight);
}
Most new machines support AVX and AVX2 these days.
__m256i unpack8_AVX2(const __m256i&xIn)
{
__m256i mRet = _mm256_unpacklo_epi8(xIn, _mm256_shuffle_epi32(xIn, _MM_SHUFFLE(3, 2, 3, 2)));
return mRet;
}
__m256i repack8_AVX2(const __m256i&xIn)
{
return unpack8_SSE(unpack8_SSE(unpack8_SSE(xIn)));
}
__m256i BitMatrixTranspose_8x8_AVX2(const __m256i &xIn)
{
const __m256i c1 = _mm256_set1_epi64x(0xAA55AA55AA55AA55LL);
const __m256i c2 = _mm256_set1_epi64x(0x00AA00AA00AA00AALL);
const __m256i c3 = _mm256_set1_epi64x(0xCCCC3333CCCC3333LL);
const __m256i c4 = _mm256_set1_epi64x(0x0000CCCC0000CCCCLL);
const __m256i c5 = _mm256_set1_epi64x(0xF0F0F0F00F0F0F0FLL);
const __m256i c6 = _mm256_set1_epi64x(0x00000000F0F0F0F0LL);
const __m256i x1 = _mm256_or_si256(_mm256_and_si256(xIn, c1), _mm256_or_si256(_mm256_slli_epi64(_mm256_and_si256(xIn, c2), 7), _mm256_and_si256(_mm256_srli_epi64(xIn, 7), c2)));
const __m256i x2 = _mm256_or_si256(_mm256_and_si256(x1, c3), _mm256_or_si256(_mm256_slli_epi64(_mm256_and_si256(x1, c4), 14), _mm256_and_si256(_mm256_srli_epi64(x1, 14), c4)));
const __m256i x3 = _mm256_or_si256(_mm256_and_si256(x2, c5), _mm256_or_si256(_mm256_slli_epi64(_mm256_and_si256(x2, c6), 28), _mm256_and_si256(_mm256_srli_epi64(x2, 28), c6)));
return x3;
}
__m256i BitMatrixTranspose_16x16_AVX2(const __m256i &xIn)
{
__m256i mUnshuffle = repack8_AVX2(xIn);
__m256i mSmallTranspose= BitMatrixTranspose_8x8_AVX2(mUnshuffle);
__m256i mRet = unpack8_across_lanes_AVX2(mSmallTranspose);
return mRet;
}
This follows the same shuffle pattern used in SSE2. But the shuffle could be rewritten and simplified using the arbitrary byte shuffle instruction:
__m256i repack8_AVX2(const __m256i&xIn)
{
const __m256i xShuffleConst = _mm256_set_epi64x(0x0f0d0b0907050301LL, 0x0e0c0a0806040200LL, 0x0f0d0b0907050301LL, 0x0e0c0a0806040200LL);
__m256i mRet = _mm256_shuffle_epi8(xIn, xShuffleConst);
return mRet;
}
I would normally declare the above 256bit constant static. But it appears that MSVC doesn't handle static __m256i variables as well as it does static __m128i.
Friday, October 27, 2017
Transposing a bit matrix using SSE2
In order to make a error correcting code more resilient to burst errors, it's not uncommon to interleave bits from multiple encoded words.
Intuitively we can think of making a 2d matrix with each row being a separate codeword. Interleaving the bits is then just taking the transpose of the bit matrix.
The book "Hacker's Delight" has an ansi algorithm for transposing a 8x8 bit matrix (64 bits total):
unsigned __int64 transpose8(unsigned __int64 x)
{
x = (x & 0xAA55AA55AA55AA55LL) | ((x & 0x00AA00AA00AA00AALL) << 7) | ((x >> 7) & 0x00AA00AA00AA00AALL);
x = (x & 0xCCCC3333CCCC3333LL) | ((x & 0x0000CCCC0000CCCCLL) << 14) | ((x >> 14) & 0x0000CCCC0000CCCCLL);
x = (x & 0xF0F0F0F00F0F0F0FLL) | ((x & 0x00000000F0F0F0F0LL) << 28) | ((x >> 28) & 0x00000000F0F0F0F0LL);
return x;
}
This can be directly translated into SSE code, which will transpose two separate 8x8 matrices at the same time:
__m128i BitMatrixTranspose_8x8_SSE(const __m128i &xIn)
{
const __m128i c1 = _mm_set1_epi64x(0xAA55AA55AA55AA55LL);
const __m128i c2 = _mm_set1_epi64x(0x00AA00AA00AA00AALL);
const __m128i c3 = _mm_set1_epi64x(0xCCCC3333CCCC3333LL);
const __m128i c4 = _mm_set1_epi64x(0x0000CCCC0000CCCCLL);
const __m128i c5 = _mm_set1_epi64x(0xF0F0F0F00F0F0F0FLL);
const __m128i c6 = _mm_set1_epi64x(0x00000000F0F0F0F0LL);
const __m128i x1 = _mm_or_si128(_mm_and_si128(xIn, c1), _mm_or_si128(_mm_slli_epi64(_mm_and_si128(xIn, c2), 7), _mm_and_si128(_mm_srli_epi64(xIn, 7), c2)));
const __m128i x2 = _mm_or_si128(_mm_and_si128(x1, c3), _mm_or_si128(_mm_slli_epi64(_mm_and_si128(x1, c4), 14), _mm_and_si128(_mm_srli_epi64(x1, 14), c4)));
const __m128i x3 = _mm_or_si128(_mm_and_si128(x2, c5), _mm_or_si128(_mm_slli_epi64(_mm_and_si128(x2, c6), 28), _mm_and_si128(_mm_srli_epi64(x2, 28), c6)));
return x3;
}
A transpose operation on a square matrix is self inverse. So the above function is self inverse.
This can then be extended to take the transpose of an 8x16 matrix and a 16x8 matrix (inverse functions of each other).
__m128i unpack8_SSE(const __m128i&xIn)
{
__m128i mRet = _mm_unpacklo_epi8(xIn, _mm_shuffle_epi32(xIn, _MM_SHUFFLE(3, 2, 3, 2)));
return mRet;
}
__m128i repack8_SSE(const __m128i&xIn)
{
return unpack8_SSE(unpack8_SSE(unpack8_SSE(xIn)));
}
__m128i BitMatrixTranspose_8x16_SSE(const __m128i &xIn)
{
__m128i mTransposedHalves = BitMatrixTranspose_8x8_SSE(xIn);
__m128i mRet = unpack8_SSE(mTransposedHalves);
return mRet;
}
__m128i BitMatrixTranspose_16x8_SSE(const __m128i &xIn)
{
__m128i mUnshuffle = repack8_SSE(xIn);
__m128i mRet = BitMatrixTranspose_8x8_SSE(mUnshuffle);
return mRet;
}
It's also worth noting that unpack8_SSE and repack8_SSE are inverses of each other.
This could be simplified using the _mm_shuffle_epi8 instruction. But that's a different problem.
Intuitively we can think of making a 2d matrix with each row being a separate codeword. Interleaving the bits is then just taking the transpose of the bit matrix.
The book "Hacker's Delight" has an ansi algorithm for transposing a 8x8 bit matrix (64 bits total):
unsigned __int64 transpose8(unsigned __int64 x)
{
x = (x & 0xAA55AA55AA55AA55LL) | ((x & 0x00AA00AA00AA00AALL) << 7) | ((x >> 7) & 0x00AA00AA00AA00AALL);
x = (x & 0xCCCC3333CCCC3333LL) | ((x & 0x0000CCCC0000CCCCLL) << 14) | ((x >> 14) & 0x0000CCCC0000CCCCLL);
x = (x & 0xF0F0F0F00F0F0F0FLL) | ((x & 0x00000000F0F0F0F0LL) << 28) | ((x >> 28) & 0x00000000F0F0F0F0LL);
return x;
}
This can be directly translated into SSE code, which will transpose two separate 8x8 matrices at the same time:
__m128i BitMatrixTranspose_8x8_SSE(const __m128i &xIn)
{
const __m128i c1 = _mm_set1_epi64x(0xAA55AA55AA55AA55LL);
const __m128i c2 = _mm_set1_epi64x(0x00AA00AA00AA00AALL);
const __m128i c3 = _mm_set1_epi64x(0xCCCC3333CCCC3333LL);
const __m128i c4 = _mm_set1_epi64x(0x0000CCCC0000CCCCLL);
const __m128i c5 = _mm_set1_epi64x(0xF0F0F0F00F0F0F0FLL);
const __m128i c6 = _mm_set1_epi64x(0x00000000F0F0F0F0LL);
const __m128i x1 = _mm_or_si128(_mm_and_si128(xIn, c1), _mm_or_si128(_mm_slli_epi64(_mm_and_si128(xIn, c2), 7), _mm_and_si128(_mm_srli_epi64(xIn, 7), c2)));
const __m128i x2 = _mm_or_si128(_mm_and_si128(x1, c3), _mm_or_si128(_mm_slli_epi64(_mm_and_si128(x1, c4), 14), _mm_and_si128(_mm_srli_epi64(x1, 14), c4)));
const __m128i x3 = _mm_or_si128(_mm_and_si128(x2, c5), _mm_or_si128(_mm_slli_epi64(_mm_and_si128(x2, c6), 28), _mm_and_si128(_mm_srli_epi64(x2, 28), c6)));
return x3;
}
A transpose operation on a square matrix is self inverse. So the above function is self inverse.
This can then be extended to take the transpose of an 8x16 matrix and a 16x8 matrix (inverse functions of each other).
__m128i unpack8_SSE(const __m128i&xIn)
{
__m128i mRet = _mm_unpacklo_epi8(xIn, _mm_shuffle_epi32(xIn, _MM_SHUFFLE(3, 2, 3, 2)));
return mRet;
}
__m128i repack8_SSE(const __m128i&xIn)
{
return unpack8_SSE(unpack8_SSE(unpack8_SSE(xIn)));
}
__m128i BitMatrixTranspose_8x16_SSE(const __m128i &xIn)
{
__m128i mTransposedHalves = BitMatrixTranspose_8x8_SSE(xIn);
__m128i mRet = unpack8_SSE(mTransposedHalves);
return mRet;
}
__m128i BitMatrixTranspose_16x8_SSE(const __m128i &xIn)
{
__m128i mUnshuffle = repack8_SSE(xIn);
__m128i mRet = BitMatrixTranspose_8x8_SSE(mUnshuffle);
return mRet;
}
It's also worth noting that unpack8_SSE and repack8_SSE are inverses of each other.
This could be simplified using the _mm_shuffle_epi8 instruction. But that's a different problem.
Friday, October 6, 2017
A bitonic sorting network for 16 float in SSE2
A while back I gave source code for a 8 float bitonic sorting network.
Bitonic sorting networks can be recursively expanded to larger sorting networks. So we have the main building block for a 16 float bitonic sorting network. The two halves are sorted, then merged together.
Here's the previously seen 8 float network.
void BitonicSortingNetwork8_SSE2(const __m128 &a, const __m128 &b, __m128 &aOut, __m128 &bOut)
{
__m128 a1 = a;
__m128 b1 = b;
__m128 a1Min = _mm_min_ps(a1, b1); // 1357
__m128 b1Max = _mm_max_ps(a1, b1); // 2468
__m128 a2 = a1Min; // 1357
__m128 b2 = _mm_shuffle_ps(b1Max, b1Max, _MM_SHUFFLE(2, 3, 0, 1)); // 4286
__m128 a2Min = _mm_min_ps(a2, b2); // 1256
__m128 b2Max = _mm_max_ps(a2, b2); // 4387
__m128 a3 = _mm_shuffle_ps(a2Min, b2Max, _MM_SHUFFLE(3, 1, 2, 0)); // 1537
__m128 b3 = _mm_shuffle_ps(a2Min, b2Max, _MM_SHUFFLE(2, 0, 3, 1)); // 2648
__m128 a3Min = _mm_min_ps(a3, b3); // 1537
__m128 b3Max = _mm_max_ps(a3, b3); // 2648
__m128 a4 = a3Min; // 1537
__m128 b4 = _mm_shuffle_ps(b3Max, b3Max, _MM_SHUFFLE(0, 1, 2, 3)); // 8462
__m128 a4Min = _mm_min_ps(a4, b4); // 1432
__m128 b4Max = _mm_max_ps(a4, b4); // 8567
__m128 a5 = _mm_unpacklo_ps(a4Min, b4Max); // 1845
__m128 b5 = _mm_unpackhi_ps(a4Min, b4Max); // 3627
__m128 a5Min = _mm_min_ps(a5, b5); // 1625
__m128 b5Max = _mm_max_ps(a5, b5); // 3847
__m128 a6 = _mm_unpacklo_ps(a5Min, b5Max); // 1368
__m128 b6 = _mm_unpackhi_ps(a5Min, b5Max); // 2457
__m128 a6Min = _mm_min_ps(a6, b6); // 1357
__m128 b6Max = _mm_max_ps(a6, b6); // 2468
aOut = _mm_unpacklo_ps(a6Min, b6Max); // 1234
bOut = _mm_unpackhi_ps(a6Min, b6Max); // 5678
}
This is the topLeft group of the 16 float network. It is also the bottomLeft group of the 16 float network.
This leaves the right half. The last 3 sets of comparisons look like the last 3 comparisons of the 8 float network.
void UpperHalfRightHalfBitonicSorter_SSE2(const __m128 &aIn, const __m128 &bIn, __m128 &aOut, __m128 &bOut)
{
__m128 a1 = aIn; // 1234
__m128 b1 = bIn; // 5678
__m128 a1Min = _mm_min_ps(a1, b1); // 1234
__m128 b1Max = _mm_max_ps(a1, b1); // 5678
__m128 a2 = _mm_unpacklo_ps(a1Min, b1Max); // 1526
__m128 b2 = _mm_unpackhi_ps(a1Min, b1Max); // 3748
__m128 a2Min = _mm_min_ps(a2, b2); // 1526
__m128 b2Max = _mm_max_ps(a2, b2); // 3748
__m128 a3 = _mm_unpacklo_ps(a2Min, b2Max); // 1357
__m128 b3 = _mm_unpackhi_ps(a2Min, b2Max); // 2468
__m128 a3Min = _mm_min_ps(a3, b3); // 1357
__m128 b3Max = _mm_max_ps(a3, b3); // 2468
aOut = _mm_unpacklo_ps(a3Min, b3Max); // 1234
bOut = _mm_unpackhi_ps(a3Min, b3Max); // 5678
}
Bitonic sorting networks can be recursively expanded to larger sorting networks. So we have the main building block for a 16 float bitonic sorting network. The two halves are sorted, then merged together.
Here's the previously seen 8 float network.
void BitonicSortingNetwork8_SSE2(const __m128 &a, const __m128 &b, __m128 &aOut, __m128 &bOut)
{
__m128 a1 = a;
__m128 b1 = b;
__m128 a1Min = _mm_min_ps(a1, b1); // 1357
__m128 b1Max = _mm_max_ps(a1, b1); // 2468
__m128 a2 = a1Min; // 1357
__m128 b2 = _mm_shuffle_ps(b1Max, b1Max, _MM_SHUFFLE(2, 3, 0, 1)); // 4286
__m128 a2Min = _mm_min_ps(a2, b2); // 1256
__m128 b2Max = _mm_max_ps(a2, b2); // 4387
__m128 a3 = _mm_shuffle_ps(a2Min, b2Max, _MM_SHUFFLE(3, 1, 2, 0)); // 1537
__m128 b3 = _mm_shuffle_ps(a2Min, b2Max, _MM_SHUFFLE(2, 0, 3, 1)); // 2648
__m128 a3Min = _mm_min_ps(a3, b3); // 1537
__m128 b3Max = _mm_max_ps(a3, b3); // 2648
__m128 a4 = a3Min; // 1537
__m128 b4 = _mm_shuffle_ps(b3Max, b3Max, _MM_SHUFFLE(0, 1, 2, 3)); // 8462
__m128 a4Min = _mm_min_ps(a4, b4); // 1432
__m128 b4Max = _mm_max_ps(a4, b4); // 8567
__m128 a5 = _mm_unpacklo_ps(a4Min, b4Max); // 1845
__m128 b5 = _mm_unpackhi_ps(a4Min, b4Max); // 3627
__m128 a5Min = _mm_min_ps(a5, b5); // 1625
__m128 b5Max = _mm_max_ps(a5, b5); // 3847
__m128 a6 = _mm_unpacklo_ps(a5Min, b5Max); // 1368
__m128 b6 = _mm_unpackhi_ps(a5Min, b5Max); // 2457
__m128 a6Min = _mm_min_ps(a6, b6); // 1357
__m128 b6Max = _mm_max_ps(a6, b6); // 2468
aOut = _mm_unpacklo_ps(a6Min, b6Max); // 1234
bOut = _mm_unpackhi_ps(a6Min, b6Max); // 5678
}
This is the topLeft group of the 16 float network. It is also the bottomLeft group of the 16 float network.
This leaves the right half. The last 3 sets of comparisons look like the last 3 comparisons of the 8 float network.
void UpperHalfRightHalfBitonicSorter_SSE2(const __m128 &aIn, const __m128 &bIn, __m128 &aOut, __m128 &bOut)
{
__m128 a1 = aIn; // 1234
__m128 b1 = bIn; // 5678
__m128 a1Min = _mm_min_ps(a1, b1); // 1234
__m128 b1Max = _mm_max_ps(a1, b1); // 5678
__m128 a2 = _mm_unpacklo_ps(a1Min, b1Max); // 1526
__m128 b2 = _mm_unpackhi_ps(a1Min, b1Max); // 3748
__m128 a2Min = _mm_min_ps(a2, b2); // 1526
__m128 b2Max = _mm_max_ps(a2, b2); // 3748
__m128 a3 = _mm_unpacklo_ps(a2Min, b2Max); // 1357
__m128 b3 = _mm_unpackhi_ps(a2Min, b2Max); // 2468
__m128 a3Min = _mm_min_ps(a3, b3); // 1357
__m128 b3Max = _mm_max_ps(a3, b3); // 2468
aOut = _mm_unpacklo_ps(a3Min, b3Max); // 1234
bOut = _mm_unpackhi_ps(a3Min, b3Max); // 5678
}
And then there's the large group of 16 comparisons in the very center.
And it all gets put together.
And it all gets put together.
void BitonicSortingNetwork16_SSE2(const __m128 &aIn, const __m128 &bIn, const __m128 &cIn, const __m128 &dIn,
__m128 &aOut, __m128 &bOut, __m128 &cOut, __m128 &dOut
)
{
__m128 a1 = aIn, b1 = bIn, c1 = cIn, d1 = dIn;
__m128 a2, b2, c2, d2;
BitonicSortingNetwork8_SSE2(a1, b1, a2, b2);
BitonicSortingNetwork8_SSE2(c1, d1, c2, d2);
__m128 a3 = a2, b3 = b2;
__m128 c3 = _mm_shuffle_ps(c2, c2, _MM_SHUFFLE(0, 1, 2, 3));
__m128 d3 = _mm_shuffle_ps(d2, d2, _MM_SHUFFLE(0, 1, 2, 3));
__m128 ad3Min = _mm_min_ps(a3, d3);
__m128 ad3Max = _mm_max_ps(a3, d3);
__m128 bc3Min = _mm_min_ps(b3, c3);
__m128 bc3Max = _mm_max_ps(b3, c3);
__m128 a4 = ad3Min;
__m128 b4 = bc3Min;
__m128 c4 = _mm_shuffle_ps(bc3Max, bc3Max, _MM_SHUFFLE(0, 1, 2, 3));
__m128 d4 = _mm_shuffle_ps(ad3Max, ad3Max, _MM_SHUFFLE(0, 1, 2, 3));
UpperHalfRightHalfBitonicSorter_SSE2(a4, b4, aOut, bOut);
UpperHalfRightHalfBitonicSorter_SSE2(c4, d4, cOut, dOut);
__m128 b4 = bc3Min;
__m128 c4 = _mm_shuffle_ps(bc3Max, bc3Max, _MM_SHUFFLE(0, 1, 2, 3));
__m128 d4 = _mm_shuffle_ps(ad3Max, ad3Max, _MM_SHUFFLE(0, 1, 2, 3));
UpperHalfRightHalfBitonicSorter_SSE2(a4, b4, aOut, bOut);
UpperHalfRightHalfBitonicSorter_SSE2(c4, d4, cOut, dOut);
}
This is verified using the 0/1 method described in Knuth.
Monday, September 25, 2017
Reversing the 16bit numbers in an XMM register using SSE2 and SSSE3
A bunch of algorithms end up requiring reversing the order of a bunch of bytes. In particular I've seen this come up a lot in code to decompress GIF images. A diagonal string distance algorithm on standard char strings would require reversing a string of bytes.
But my world doesn't involve many single width strings. My world tends to have 16bit Unicode strings. So reversing a string of 16bit characters will instead come up. 16bit numbers are treated the same as 16bit Unicode characters.
This can be done just with SSE2 instructions.
__m128i _mm_reverse_epi16_SSE2(const __m128i &mToReverse)
{
__m128i mReversed_epi32 = _mm_shuffle_epi32(mToReverse, _MM_SHUFFLE(0, 1, 2, 3));
__m128i mLowDone = _mm_shufflelo_epi16(mReversed_epi32, _MM_SHUFFLE(2, 3, 0, 1));
__m128i mResult = _mm_shufflehi_epi16(mLowDone, _MM_SHUFFLE(2, 3, 0, 1));
return mResult;
}
But in fact can be done in a single instruction in SSSE3 (since the pshufb instruction supports using a memory address for the second parameter).
__m128i _mm_reverse_epi16_SSSE3(const __m128i &mToReverse)
{
static const __m128i reverseKeys = { 14,15,12,13,10,11,8,9,6,7,4,5,2,3,0,1 };
__m128i mResult = _mm_shuffle_epi8(mToReverse, reverseKeys);
return mResult;
}
This is satisfying.
But my world doesn't involve many single width strings. My world tends to have 16bit Unicode strings. So reversing a string of 16bit characters will instead come up. 16bit numbers are treated the same as 16bit Unicode characters.
This can be done just with SSE2 instructions.
__m128i _mm_reverse_epi16_SSE2(const __m128i &mToReverse)
{
__m128i mReversed_epi32 = _mm_shuffle_epi32(mToReverse, _MM_SHUFFLE(0, 1, 2, 3));
__m128i mLowDone = _mm_shufflelo_epi16(mReversed_epi32, _MM_SHUFFLE(2, 3, 0, 1));
__m128i mResult = _mm_shufflehi_epi16(mLowDone, _MM_SHUFFLE(2, 3, 0, 1));
return mResult;
}
But in fact can be done in a single instruction in SSSE3 (since the pshufb instruction supports using a memory address for the second parameter).
__m128i _mm_reverse_epi16_SSSE3(const __m128i &mToReverse)
{
static const __m128i reverseKeys = { 14,15,12,13,10,11,8,9,6,7,4,5,2,3,0,1 };
__m128i mResult = _mm_shuffle_epi8(mToReverse, reverseKeys);
return mResult;
}
This is satisfying.
Sunday, September 24, 2017
Levenshtein distance calculated on the diagonal (but only in ANSI for now)
A long time ago I promised to talk about a better way of calculating Levenshtein distance (edit distance). A way that is more conducive to vectorization.
The trick is to calculate the same edit distance matrix as the standard two row method, but instead fill in the values in a diagonal manner.
This ends up having each diagonal depending on the previous two diagonals. But importantly each diagonal does not depend on any other element of itself.
size_t Levenshtein_distance_diagonal_ANSI(const wchar_t* const s, const wchar_t* const t)
{
const unsigned int lenS = wcslen(s);
const unsigned int lenT = wcslen(t);
if (0 == lenS)
{
return lenT;
}
if (0 == lenT)
{
return lenS;
}
if (0 == wcscmp(s, t))
{
return 0;
}
// create work vectors of integer distances
unsigned int *v0 = new unsigned int[lenT + 1];
unsigned int *v1 = new unsigned int[lenT + 1];
unsigned int *v2 = new unsigned int[lenT + 1];
v1[0] = 0;
for (unsigned int j =1; j <= (lenS+lenT); j++)
{
unsigned int iMin;
unsigned int iMax;
v2[0] = j * 1;
iMin = (unsigned int)max(1, (int)(j - lenS));
if (j <= lenT)
{
v2[j] = j * 1;
iMax = j-1;
}
else
{
iMax = lenT;
}
for (unsigned int i = iMin; i <= iMax; i++)
{
unsigned int substituteCost = v0[i-1]+(s[j-i-1] != t[i-1]);
unsigned int insertionCost = v1[i-1]+1;
unsigned int deletionCost = v1[i]+1;
v2[i] = min(min(substituteCost, insertionCost), deletionCost);
}
unsigned int * const vTemp = v0;
v0 = v1;
v1 = v2;
v2 = vTemp;
}
unsigned int retVal = v1[lenT];
delete[] v0;
delete[] v1;
delete[] v2;
return retVal;
}
While this implementation is not any better than the two row implementation, we can see where this is going.
This also can work with storage only for two diagonals, overwriting a diagonal just after its value is read.
The trick is to calculate the same edit distance matrix as the standard two row method, but instead fill in the values in a diagonal manner.
This ends up having each diagonal depending on the previous two diagonals. But importantly each diagonal does not depend on any other element of itself.
size_t Levenshtein_distance_diagonal_ANSI(const wchar_t* const s, const wchar_t* const t)
{
const unsigned int lenS = wcslen(s);
const unsigned int lenT = wcslen(t);
if (0 == lenS)
{
return lenT;
}
if (0 == lenT)
{
return lenS;
}
if (0 == wcscmp(s, t))
{
return 0;
}
// create work vectors of integer distances
unsigned int *v0 = new unsigned int[lenT + 1];
unsigned int *v1 = new unsigned int[lenT + 1];
unsigned int *v2 = new unsigned int[lenT + 1];
v1[0] = 0;
for (unsigned int j =1; j <= (lenS+lenT); j++)
{
unsigned int iMin;
unsigned int iMax;
v2[0] = j * 1;
iMin = (unsigned int)max(1, (int)(j - lenS));
if (j <= lenT)
{
v2[j] = j * 1;
iMax = j-1;
}
else
{
iMax = lenT;
}
for (unsigned int i = iMin; i <= iMax; i++)
{
unsigned int substituteCost = v0[i-1]+(s[j-i-1] != t[i-1]);
unsigned int insertionCost = v1[i-1]+1;
unsigned int deletionCost = v1[i]+1;
v2[i] = min(min(substituteCost, insertionCost), deletionCost);
}
unsigned int * const vTemp = v0;
v0 = v1;
v1 = v2;
v2 = vTemp;
}
unsigned int retVal = v1[lenT];
delete[] v0;
delete[] v1;
delete[] v2;
return retVal;
}
While this implementation is not any better than the two row implementation, we can see where this is going.
This also can work with storage only for two diagonals, overwriting a diagonal just after its value is read.
Tuesday, August 22, 2017
Another 4 element DCT_II - this time in transpose
There are some fun optimizations that can be done for the DCT(type 2 in this case) for striped input.
The striped input version takes as input and produces the output that is the transpose of four separate standard DCT calls.
While striping may seem like an esoteric way of doing things, the transpose is going to be a big part of 2-dimensional DCT, so this doesn't impose much additional work.
void DCT_II_T( __m128 & mInOutTA, __m128 & mInOutTB, __m128 & mInOutTC, __m128 & mInOutTD)
{
__declspec(align(16)) static const float aDctCoefs[] = {
0.5000000000000000f, 0.4619397662556434f, 0.3535533905932738f, 0.1913417161825449f };
__m128 mTApTD = _mm_add_ps(mInOutTA, mInOutTD);
__m128 mTAsTD = _mm_sub_ps(mInOutTA, mInOutTD);
__m128 mTBpTC = _mm_add_ps(mInOutTB, mInOutTC);
__m128 mTBsTC = _mm_sub_ps(mInOutTB, mInOutTC);
__m128 mResultTA = _mm_mul_ps(_mm_set1_ps(aDctCoefs[0]), _mm_add_ps(mTApTD, mTBpTC));
__m128 mResultTB = _mm_add_ps(_mm_mul_ps(_mm_set1_ps(aDctCoefs[1]), mTAsTD),_mm_mul_ps(_mm_set1_ps(aDctCoefs[3]), mTBsTC));
__m128 mResultTC = _mm_mul_ps(_mm_set1_ps(aDctCoefs[2]), _mm_sub_ps(mTApTD, mTBpTC));
__m128 mResultTD = _mm_sub_ps(_mm_mul_ps(_mm_set1_ps(aDctCoefs[3]), mTAsTD), _mm_mul_ps(_mm_set1_ps(aDctCoefs[1]), mTBsTC));
mInOutTA = mResultTA;
mInOutTB = mResultTB;
mInOutTC = mResultTC;
mInOutTD = mResultTD;
}
The baseline implementation took 4 multiplies and 3 adds. The above implementation takes 8 adds and 6 multiples to do 4 times as much work (also less space is taken up by constants).
The striped input version takes as input and produces the output that is the transpose of four separate standard DCT calls.
While striping may seem like an esoteric way of doing things, the transpose is going to be a big part of 2-dimensional DCT, so this doesn't impose much additional work.
void DCT_II_T( __m128 & mInOutTA, __m128 & mInOutTB, __m128 & mInOutTC, __m128 & mInOutTD)
{
__declspec(align(16)) static const float aDctCoefs[] = {
0.5000000000000000f, 0.4619397662556434f, 0.3535533905932738f, 0.1913417161825449f };
__m128 mTApTD = _mm_add_ps(mInOutTA, mInOutTD);
__m128 mTAsTD = _mm_sub_ps(mInOutTA, mInOutTD);
__m128 mTBpTC = _mm_add_ps(mInOutTB, mInOutTC);
__m128 mTBsTC = _mm_sub_ps(mInOutTB, mInOutTC);
__m128 mResultTA = _mm_mul_ps(_mm_set1_ps(aDctCoefs[0]), _mm_add_ps(mTApTD, mTBpTC));
__m128 mResultTB = _mm_add_ps(_mm_mul_ps(_mm_set1_ps(aDctCoefs[1]), mTAsTD),_mm_mul_ps(_mm_set1_ps(aDctCoefs[3]), mTBsTC));
__m128 mResultTC = _mm_mul_ps(_mm_set1_ps(aDctCoefs[2]), _mm_sub_ps(mTApTD, mTBpTC));
__m128 mResultTD = _mm_sub_ps(_mm_mul_ps(_mm_set1_ps(aDctCoefs[3]), mTAsTD), _mm_mul_ps(_mm_set1_ps(aDctCoefs[1]), mTBsTC));
mInOutTA = mResultTA;
mInOutTB = mResultTB;
mInOutTC = mResultTC;
mInOutTD = mResultTD;
}
The baseline implementation took 4 multiplies and 3 adds. The above implementation takes 8 adds and 6 multiples to do 4 times as much work (also less space is taken up by constants).
Sunday, July 9, 2017
A basic implementation of a 4-element Discreet Cosine Transform in SSE
The discreet cosine transform (DCT) comes up a lot in graphics and sound processing. These will often be done with a relative of the FFT.
The inverse of the DCT is a slightly different DCT. (DCT type 2 is the inverse of DCT type 3 and vice versa)
A four element DCT is almost trivially small, but I think that it will offer opportunities for a variety of interesting optimizations.
The DCT is linear, so a 4 element transform can be written as a multiplication by a 4x4 matrix.
A straightforward implementation follows.
__m128 DCT_II(const __m128 mIn)
{
__declspec(align(16)) static const float mDctMatrix[] = { 0.5000000000000000f, 0.4619397662556434f, 0.3535533905932738f, \
0.1913417161825449f, 0.5000000000000000f, 0.1913417161825449f, \
- 0.3535533905932738f, -0.4619397662556434f, 0.5000000000000000f, \
- 0.1913417161825449f, -0.3535533905932738f, 0.4619397662556434f, \
0.5000000000000000f, -0.4619397662556434f, 0.3535533905932738f, \
- 0.1913417161825449f };
__m128 mProd0 = _mm_mul_ps(_mm_shuffle_ps(mIn, mIn, _MM_SHUFFLE(0, 0, 0, 0)), _mm_load_ps(&mDctMatrix[0]));
__m128 mProd1 = _mm_mul_ps(_mm_shuffle_ps(mIn, mIn, _MM_SHUFFLE(1, 1, 1, 1)), _mm_load_ps(&mDctMatrix[4]));
__m128 mProd2 = _mm_mul_ps(_mm_shuffle_ps(mIn, mIn, _MM_SHUFFLE(2, 2, 2, 2)), _mm_load_ps(&mDctMatrix[8]));
__m128 mProd3 = _mm_mul_ps(_mm_shuffle_ps(mIn, mIn, _MM_SHUFFLE(3, 3, 3, 3)), _mm_load_ps(&mDctMatrix[12]));
return _mm_add_ps(_mm_add_ps(mProd0, mProd1), _mm_add_ps(mProd2, mProd3));
}
and its inverse:
__m128 DCT_III(const __m128 mIn)
{
__declspec(align(16)) static const float mDctMatrix[] = { 0.5000000000000000f, 0.5000000000000000f, 0.5000000000000000f, \
0.5000000000000000f, 0.9238795325112868f, 0.3826834323650898f, \
- 0.3826834323650898f, -0.9238795325112868f, 0.7071067811865475f, \
- 0.7071067811865475f, -0.7071067811865475f, 0.7071067811865475f, \
0.3826834323650898f, -0.9238795325112868f, 0.9238795325112868f, \
- 0.3826834323650898f };
__m128 mProd0 = _mm_mul_ps(_mm_shuffle_ps(mIn, mIn, _MM_SHUFFLE(0, 0, 0, 0)), _mm_load_ps(&mDctMatrix[0]));
__m128 mProd1 = _mm_mul_ps(_mm_shuffle_ps(mIn, mIn, _MM_SHUFFLE(1, 1, 1, 1)), _mm_load_ps(&mDctMatrix[4]));
__m128 mProd2 = _mm_mul_ps(_mm_shuffle_ps(mIn, mIn, _MM_SHUFFLE(2, 2, 2, 2)), _mm_load_ps(&mDctMatrix[8]));
__m128 mProd3 = _mm_mul_ps(_mm_shuffle_ps(mIn, mIn, _MM_SHUFFLE(3, 3, 3, 3)), _mm_load_ps(&mDctMatrix[12]));
return _mm_add_ps(_mm_add_ps(mProd0, mProd1), _mm_add_ps(mProd2, mProd3));
}
There are opportunities for optimization here that I will be revisiting.
The inverse of the DCT is a slightly different DCT. (DCT type 2 is the inverse of DCT type 3 and vice versa)
A four element DCT is almost trivially small, but I think that it will offer opportunities for a variety of interesting optimizations.
The DCT is linear, so a 4 element transform can be written as a multiplication by a 4x4 matrix.
A straightforward implementation follows.
__m128 DCT_II(const __m128 mIn)
{
__declspec(align(16)) static const float mDctMatrix[] = { 0.5000000000000000f, 0.4619397662556434f, 0.3535533905932738f, \
0.1913417161825449f, 0.5000000000000000f, 0.1913417161825449f, \
- 0.3535533905932738f, -0.4619397662556434f, 0.5000000000000000f, \
- 0.1913417161825449f, -0.3535533905932738f, 0.4619397662556434f, \
0.5000000000000000f, -0.4619397662556434f, 0.3535533905932738f, \
- 0.1913417161825449f };
__m128 mProd0 = _mm_mul_ps(_mm_shuffle_ps(mIn, mIn, _MM_SHUFFLE(0, 0, 0, 0)), _mm_load_ps(&mDctMatrix[0]));
__m128 mProd1 = _mm_mul_ps(_mm_shuffle_ps(mIn, mIn, _MM_SHUFFLE(1, 1, 1, 1)), _mm_load_ps(&mDctMatrix[4]));
__m128 mProd2 = _mm_mul_ps(_mm_shuffle_ps(mIn, mIn, _MM_SHUFFLE(2, 2, 2, 2)), _mm_load_ps(&mDctMatrix[8]));
__m128 mProd3 = _mm_mul_ps(_mm_shuffle_ps(mIn, mIn, _MM_SHUFFLE(3, 3, 3, 3)), _mm_load_ps(&mDctMatrix[12]));
return _mm_add_ps(_mm_add_ps(mProd0, mProd1), _mm_add_ps(mProd2, mProd3));
}
and its inverse:
__m128 DCT_III(const __m128 mIn)
{
__declspec(align(16)) static const float mDctMatrix[] = { 0.5000000000000000f, 0.5000000000000000f, 0.5000000000000000f, \
0.5000000000000000f, 0.9238795325112868f, 0.3826834323650898f, \
- 0.3826834323650898f, -0.9238795325112868f, 0.7071067811865475f, \
- 0.7071067811865475f, -0.7071067811865475f, 0.7071067811865475f, \
0.3826834323650898f, -0.9238795325112868f, 0.9238795325112868f, \
- 0.3826834323650898f };
__m128 mProd0 = _mm_mul_ps(_mm_shuffle_ps(mIn, mIn, _MM_SHUFFLE(0, 0, 0, 0)), _mm_load_ps(&mDctMatrix[0]));
__m128 mProd1 = _mm_mul_ps(_mm_shuffle_ps(mIn, mIn, _MM_SHUFFLE(1, 1, 1, 1)), _mm_load_ps(&mDctMatrix[4]));
__m128 mProd2 = _mm_mul_ps(_mm_shuffle_ps(mIn, mIn, _MM_SHUFFLE(2, 2, 2, 2)), _mm_load_ps(&mDctMatrix[8]));
__m128 mProd3 = _mm_mul_ps(_mm_shuffle_ps(mIn, mIn, _MM_SHUFFLE(3, 3, 3, 3)), _mm_load_ps(&mDctMatrix[12]));
return _mm_add_ps(_mm_add_ps(mProd0, mProd1), _mm_add_ps(mProd2, mProd3));
}
There are opportunities for optimization here that I will be revisiting.
Using the inverse square root to calculate 2d normal vectors in SSE
The inverse square root (1/√x) comes up in computer graphics. This particularly comes up in the calculation of unit direction vectors. Game graphics have famously used a low-precision fast version.
We can calculate the unit direction vector for two separate vectors at the same time.
template<bool bUseFasterButLessAccurate>
__m128 directionVectorsSSE(const __m128 &mIn)
{
__m128 mInSq = _mm_mul_ps(mIn, mIn);
__m128 mHorizontalSumSq = _mm_add_ps(mInSq, _mm_shuffle_ps(mInSq, mInSq, _MM_SHUFFLE(2, 3, 0, 1)));
__m128 mScaled;
if (bUseFasterButLessAccurate)
{
__m128 mRsqrt = _mm_rsqrt_ps(mHorizontalSumSq);
mScaled = _mm_mul_ps(mIn, mRsqrt);
}
else
{
__m128 mSqrt = _mm_sqrt_ps(mHorizontalSumSq);
mScaled = _mm_div_ps(mIn, mSqrt);
}
__m128 mIsZero = _mm_cmpgt_ps(mHorizontalSumSq, _mm_setzero_ps());
__m128 mScaledIsZero = _mm_and_ps(mScaled, mIsZero);
return mScaledIsZero;
}
This will use either the direct calculation or less accurate version based on the template parameter.
It seems like there should be a way to make use of the actual horizontal sum instruction, but that would just move the required shuffle, so does not benefit the code.
We do have a division by something that could be zero. We don't want to return NaN for a zero input vector. The above code handles this by returning a zero vector by and'ing the division against the bit result of a comparison.
We can calculate the unit direction vector for two separate vectors at the same time.
template<bool bUseFasterButLessAccurate>
__m128 directionVectorsSSE(const __m128 &mIn)
{
__m128 mInSq = _mm_mul_ps(mIn, mIn);
__m128 mHorizontalSumSq = _mm_add_ps(mInSq, _mm_shuffle_ps(mInSq, mInSq, _MM_SHUFFLE(2, 3, 0, 1)));
__m128 mScaled;
if (bUseFasterButLessAccurate)
{
__m128 mRsqrt = _mm_rsqrt_ps(mHorizontalSumSq);
mScaled = _mm_mul_ps(mIn, mRsqrt);
}
else
{
__m128 mSqrt = _mm_sqrt_ps(mHorizontalSumSq);
mScaled = _mm_div_ps(mIn, mSqrt);
}
__m128 mIsZero = _mm_cmpgt_ps(mHorizontalSumSq, _mm_setzero_ps());
__m128 mScaledIsZero = _mm_and_ps(mScaled, mIsZero);
return mScaledIsZero;
}
This will use either the direct calculation or less accurate version based on the template parameter.
It seems like there should be a way to make use of the actual horizontal sum instruction, but that would just move the required shuffle, so does not benefit the code.
We do have a division by something that could be zero. We don't want to return NaN for a zero input vector. The above code handles this by returning a zero vector by and'ing the division against the bit result of a comparison.
Wednesday, May 31, 2017
a 2d horizontal sum in SSE2
2d vectors come up a lot in graphics. Floats are treated in pairs with all of the normal linear algebra operations.
Adding four scaled 2d vectors is a straightforward operation.
We pass in the 2d vectors in 2 XMM registers, and the four element scaling values in a single XMM register.
__forceinline __m128 horizontalSum2D_SSE2(const __m128 mLeft, const __m128 mRight)
{
__m128 mTop = _mm_add_ps(mLeft, mRight);
__m128 mShuffleTop = _mm_shuffle_ps(mTop, mTop, _MM_SHUFFLE(1, 0, 3, 2));
__m128 mRet = _mm_add_ps(mTop, mShuffleTop);
return mRet;
}
__m128 scaleHorizontalSum2D_SSE2(const __m128 mLeft, const __m128 mRight, const __m128 mScales)
{
__m128 mScaleLeft = _mm_unpacklo_ps(mScales, mScales);
__m128 mScaleRight = _mm_unpackhi_ps(mScales, mScales);
__m128 mMulLeft = _mm_mul_ps(mScaleLeft, mLeft);
__m128 mMulRight = _mm_mul_ps(mScaleRight, mRight);
__m128 mRet = horizontalSum2D_SSE2(mMulLeft, mMulRight);
return mRet;
}
The result is returned in the an XMM register. This entire operation takes only 9 instructions.
Adding four scaled 2d vectors is a straightforward operation.
We pass in the 2d vectors in 2 XMM registers, and the four element scaling values in a single XMM register.
__forceinline __m128 horizontalSum2D_SSE2(const __m128 mLeft, const __m128 mRight)
{
__m128 mTop = _mm_add_ps(mLeft, mRight);
__m128 mShuffleTop = _mm_shuffle_ps(mTop, mTop, _MM_SHUFFLE(1, 0, 3, 2));
__m128 mRet = _mm_add_ps(mTop, mShuffleTop);
return mRet;
}
__m128 scaleHorizontalSum2D_SSE2(const __m128 mLeft, const __m128 mRight, const __m128 mScales)
{
__m128 mScaleLeft = _mm_unpacklo_ps(mScales, mScales);
__m128 mScaleRight = _mm_unpackhi_ps(mScales, mScales);
__m128 mMulLeft = _mm_mul_ps(mScaleLeft, mLeft);
__m128 mMulRight = _mm_mul_ps(mScaleRight, mRight);
__m128 mRet = horizontalSum2D_SSE2(mMulLeft, mMulRight);
return mRet;
}
The result is returned in the an XMM register. This entire operation takes only 9 instructions.
Monday, May 29, 2017
float bilinear interpolation using SSE2
Bilinear interpolation is an easy way to smooth out sampled data. The sampled value is known at the corners of the unit square. Interpolation is performed linearly in each dimension.
Basically this boils down to evaluating the function:

void bilinearInterpolate_ANSI(__in_ecount(2) const float * const pXY, __in_ecount(2) const float *const pF0, __in_ecount(2) const float *const pF1, __out float *const pResult)
{
const float &x = pXY[0];
const float &y = pXY[1];
*pResult = pF0[0] * (1 - x)*(1 - y) + pF0[1] * x*(1 - y) + pF1[0] * (1 - x)*y + pF1[1] * x*y;
}
That addition is either going to require a horizontal add, or will require something like a transpose for the functional values. I've chosen to go with the horizontal addition route.
For the moment, let's look at everything up to multiplying by the f values. It's another case where it's close to the same cost to evaluate two as to evaluate one.
void bilinearInterpolateInner_SSE(const __m128 &mXY, __out __m128 &mLeft, __out __m128 &mRight)
{
__m128 m1111 = _mm_set1_ps(1);
__m128 mOmXY = _mm_sub_ps(m1111, mXY);
__m128 mYLeft = _mm_shuffle_ps(mOmXY, mXY, _MM_SHUFFLE(1, 1, 1, 1));
__m128 mYRight = _mm_shuffle_ps(mOmXY, mXY, _MM_SHUFFLE(3, 3, 3, 3));
__m128 mXYOmXYLeft = _mm_unpacklo_ps(mXY, mOmXY);
__m128 mXYOmXYRight = _mm_unpackhi_ps(mXY, mOmXY);
__m128 mXLeft = _mm_shuffle_ps(mXYOmXYLeft, mXYOmXYLeft, _MM_SHUFFLE(0, 1, 0, 1));
__m128 mXRight = _mm_shuffle_ps(mXYOmXYRight, mXYOmXYRight, _MM_SHUFFLE(0, 1, 0, 1));
mLeft = _mm_mul_ps(mXLeft, mYLeft);
mRight = _mm_mul_ps(mXRight, mYRight);
}
If we have loaded the values for f into two SSE registers, this can be evaluated as follows:
__forceinline __m128 _mm_hadd_ps_SSE2(const __m128 mLeft, const __m128 mRight)
{
__m128 mTop = _mm_shuffle_ps(mLeft, mRight, _MM_SHUFFLE(0, 2, 0, 2));
__m128 mBottom = _mm_shuffle_ps(mLeft, mRight, _MM_SHUFFLE(1, 3, 1, 3));
return _mm_add_ps(mTop, mBottom);
}
__forceinline void store2floats(const __m128 &mFloats, __out_ecount(2) float * const pfResults)
{
_mm_store_sd(reinterpret_cast<double *>(pfResults), _mm_castps_pd(mFloats));
}
void bilinearInterpolateMiddle_SSE(const __m128 &mXYLeftRight, const __m128 &mFLeft, const __m128 &mFRight, __out_ecount(2) float * const pfResults)
{
__m128 mLeft, mRight;
bilinearInterpolateInner_SSE(mXYLeftRight, mLeft, mRight);
__m128 mInt = _mm_hadd_ps_SSE2(_mm_mul_ps(mRight,mFRight),_mm_mul_ps(mLeft,mFLeft));
__m128 mRet = _mm_hadd_ps_SSE2(mInt, mInt);
store2floats(mRet, pfResults);
}
This does the final multiply against the f values. And then does the horizontal sum. The two horizontal sums are performed simultaneously. The SSE3 _mm_hadd_ps instruction would be helpful, but it is sumulated using SSE2 in the above example.
Basically this boils down to evaluating the function:

void bilinearInterpolate_ANSI(__in_ecount(2) const float * const pXY, __in_ecount(2) const float *const pF0, __in_ecount(2) const float *const pF1, __out float *const pResult)
{
const float &x = pXY[0];
const float &y = pXY[1];
*pResult = pF0[0] * (1 - x)*(1 - y) + pF0[1] * x*(1 - y) + pF1[0] * (1 - x)*y + pF1[1] * x*y;
}
That addition is either going to require a horizontal add, or will require something like a transpose for the functional values. I've chosen to go with the horizontal addition route.
For the moment, let's look at everything up to multiplying by the f values. It's another case where it's close to the same cost to evaluate two as to evaluate one.
void bilinearInterpolateInner_SSE(const __m128 &mXY, __out __m128 &mLeft, __out __m128 &mRight)
{
__m128 m1111 = _mm_set1_ps(1);
__m128 mOmXY = _mm_sub_ps(m1111, mXY);
__m128 mYLeft = _mm_shuffle_ps(mOmXY, mXY, _MM_SHUFFLE(1, 1, 1, 1));
__m128 mYRight = _mm_shuffle_ps(mOmXY, mXY, _MM_SHUFFLE(3, 3, 3, 3));
__m128 mXYOmXYLeft = _mm_unpacklo_ps(mXY, mOmXY);
__m128 mXYOmXYRight = _mm_unpackhi_ps(mXY, mOmXY);
__m128 mXLeft = _mm_shuffle_ps(mXYOmXYLeft, mXYOmXYLeft, _MM_SHUFFLE(0, 1, 0, 1));
__m128 mXRight = _mm_shuffle_ps(mXYOmXYRight, mXYOmXYRight, _MM_SHUFFLE(0, 1, 0, 1));
mLeft = _mm_mul_ps(mXLeft, mYLeft);
mRight = _mm_mul_ps(mXRight, mYRight);
}
If we have loaded the values for f into two SSE registers, this can be evaluated as follows:
__forceinline __m128 _mm_hadd_ps_SSE2(const __m128 mLeft, const __m128 mRight)
{
__m128 mTop = _mm_shuffle_ps(mLeft, mRight, _MM_SHUFFLE(0, 2, 0, 2));
__m128 mBottom = _mm_shuffle_ps(mLeft, mRight, _MM_SHUFFLE(1, 3, 1, 3));
return _mm_add_ps(mTop, mBottom);
}
__forceinline void store2floats(const __m128 &mFloats, __out_ecount(2) float * const pfResults)
{
_mm_store_sd(reinterpret_cast<double *>(pfResults), _mm_castps_pd(mFloats));
}
void bilinearInterpolateMiddle_SSE(const __m128 &mXYLeftRight, const __m128 &mFLeft, const __m128 &mFRight, __out_ecount(2) float * const pfResults)
{
__m128 mLeft, mRight;
bilinearInterpolateInner_SSE(mXYLeftRight, mLeft, mRight);
__m128 mInt = _mm_hadd_ps_SSE2(_mm_mul_ps(mRight,mFRight),_mm_mul_ps(mLeft,mFLeft));
__m128 mRet = _mm_hadd_ps_SSE2(mInt, mInt);
store2floats(mRet, pfResults);
}
This does the final multiply against the f values. And then does the horizontal sum. The two horizontal sums are performed simultaneously. The SSE3 _mm_hadd_ps instruction would be helpful, but it is sumulated using SSE2 in the above example.
Saturday, May 13, 2017
The preprocessing for a box blur in SSE2. The sum of all of the elements in a 2d array above and to to the left.
It is often useful to blur images. It is often to blur the same image in multiple ways. A common way of doing this is to precalculate a resulting intermediate and then quickly produce multiple resulting blurred images.
The preprocess is create an array of floats in the shape of the image. The value at each location is the inclusive sum of all of the values from the original image all the way to the upper left pixel of the image above and to the left of the target point.
This process pretty easy suffers from integer overflow, so we need to use floats in the intermediate image.
We saw a 1-dimensional cumulative sum in a previous post. And that is re-included here.
template <typename T>
__forceinline T SumArray(__in_ecount(cElements) const T * const aIn, __out_ecount(cElements) T* const aOut, const size_t cElements, const T fRunningSumIn = 0)
{
T fRunningSum = fRunningSumIn;
for (size_t iOnElement = 0; iOnElement < cElements; iOnElement++)
{
aOut[iOnElement] = (fRunningSum += aIn[iOnElement]);
}
return fRunningSum;
}
template<const unsigned char nElementsToShift>
__forceinline __m128 _mm_slli_ps(__m128 m)
{
return _mm_castsi128_ps(_mm_slli_si128(_mm_castps_si128(m), 4 * nElementsToShift));
}
__forceinline __m128 SumRegister(__m128 mIn)
{
__m128 mAddShift = _mm_add_ps(mIn, _mm_slli_ps<1>(mIn));
return _mm_add_ps(mAddShift, _mm_slli_ps<2>(mAddShift));
}
float CumulativeSum_SSE(const float * const aIn, float * const aOut, size_t cElements, float fRunningSum = 0)
{
size_t cOnElement = cElements & 3;
fRunningSum = SumArray(aIn, aOut, cOnElement, fRunningSum);
__m128 mLeftSum = _mm_set1_ps(fRunningSum);
if (cElements & 4)
{
__m128 mIn = _mm_loadu_ps(aIn + cOnElement);
__m128 mOut = _mm_add_ps(mLeftSum, SumRegister(mIn));
_mm_storeu_ps(aOut + cOnElement, mOut);
mLeftSum = _mm_shuffle_ps(mOut, mOut, _MM_SHUFFLE(3, 3, 3, 3));
cOnElement += 4;
}
while (cOnElement<cElements)
{
__m128 mInLo = _mm_loadu_ps(aIn + cOnElement);
__m128 mInHi = _mm_loadu_ps(aIn + cOnElement + 4);
__m128 mSummedInLo = SumRegister(mInLo);
__m128 mSummedInHi = SumRegister(mInHi);
__m128 mOutLo = _mm_add_ps(mLeftSum, mSummedInLo);
_mm_storeu_ps(aOut + cOnElement, mOutLo);
mLeftSum = _mm_shuffle_ps(mOutLo, mOutLo, _MM_SHUFFLE(3, 3, 3, 3));
__m128 mOutHi = _mm_add_ps(mLeftSum, mSummedInHi);
_mm_storeu_ps(aOut + cOnElement + 4, mOutHi);
mLeftSum = _mm_shuffle_ps(mOutHi, mOutHi, _MM_SHUFFLE(3, 3, 3, 3));
cOnElement += 8;
}
return _mm_cvtss_f32(mLeftSum);
}
And then the 2-dimensional summation will look pretty similar:
void BoxFilterPreCalc_SSE(const float * const aIn, float * const aOut, const size_t cHorizontalElements, const size_t cVerticalElements, const ptrdiff_t verticalStrideIn, const ptrdiff_t verticalStrideOut)
{
if (!cVerticalElements)
{
return;
}
CumulativeSum_SSE(aIn, aOut, cHorizontalElements, 0);
size_t cRowsRemaining = cVerticalElements - 1;
const float *pStartOutPrevLine = aOut;
float *pStartOutCurLine = AddBytesToPointer(aOut, verticalStrideOut);
const float *pStartInCurLine = AddBytesToPointer(aIn, verticalStrideIn);
while (cRowsRemaining-- > 0)
{
float fLeftSum = 0;
size_t iOnElement = 0;
size_t cElementsRemaining = cHorizontalElements;
while (cElementsRemaining & 3)
{
cElementsRemaining--;
pStartOutCurLine[iOnElement] = pStartOutPrevLine[iOnElement]+(fLeftSum += pStartInCurLine[iOnElement]);
iOnElement++;
}
__m128 mLeftSum = _mm_set1_ps(fLeftSum);
if (cElementsRemaining & 4)
{
cElementsRemaining -= 4;
__m128 mInLo = _mm_loadu_ps(pStartInCurLine + iOnElement);
__m128 mPrevOutLo = _mm_loadu_ps(pStartOutPrevLine + iOnElement);
__m128 mSummedInLo = SumRegister(mInLo);
__m128 mLeftSumOutLo = _mm_add_ps(mLeftSum, mSummedInLo);
__m128 mOutLo = _mm_add_ps(mLeftSumOutLo, mPrevOutLo);
_mm_storeu_ps(pStartOutCurLine + iOnElement, mOutLo);
mLeftSum = _mm_shuffle_ps(mLeftSumOutLo, mLeftSumOutLo, _MM_SHUFFLE(3, 3, 3, 3));
iOnElement += 4;
}
while (cElementsRemaining > 0)
{
cElementsRemaining -= 8;
__m128 mInLo = _mm_loadu_ps(pStartInCurLine + iOnElement);
__m128 mInHi = _mm_loadu_ps(pStartInCurLine + iOnElement + 4);
__m128 mPrevOutLo = _mm_loadu_ps(pStartOutPrevLine + iOnElement);
__m128 mPrevOutHi = _mm_loadu_ps(pStartOutPrevLine + iOnElement+4);
__m128 mSummedInLo = SumRegister(mInLo);
__m128 mSummedInHi = SumRegister(mInHi);
__m128 mLeftSumOutLo = _mm_add_ps(mLeftSum, mSummedInLo);
__m128 mOutLo = _mm_add_ps(mLeftSumOutLo, mPrevOutLo);
_mm_storeu_ps(pStartOutCurLine + iOnElement, mOutLo);
__m128 mLeftSum = _mm_shuffle_ps(mLeftSumOutLo, mLeftSumOutLo, _MM_SHUFFLE(3, 3, 3, 3));
__m128 mLeftSumOutHi = _mm_add_ps(mLeftSum, mSummedInHi);
__m128 mOutHi = _mm_add_ps(mLeftSumOutHi, mPrevOutHi);
_mm_storeu_ps(pStartOutCurLine + iOnElement + 4, mOutHi);
mLeftSum = _mm_shuffle_ps(mLeftSumOutHi, mLeftSumOutHi, _MM_SHUFFLE(3, 3, 3, 3));
iOnElement += 8;
}
pStartOutPrevLine = pStartOutCurLine;
pStartOutCurLine = AddBytesToPointer(pStartOutCurLine, verticalStrideOut);
pStartInCurLine = AddBytesToPointer(pStartInCurLine, verticalStrideIn);
}
}
For some similar opterations we will actually legitimately need the increased accuracy of doubles. That's coming soon.
The preprocess is create an array of floats in the shape of the image. The value at each location is the inclusive sum of all of the values from the original image all the way to the upper left pixel of the image above and to the left of the target point.
This process pretty easy suffers from integer overflow, so we need to use floats in the intermediate image.
We saw a 1-dimensional cumulative sum in a previous post. And that is re-included here.
template <typename T>
__forceinline T SumArray(__in_ecount(cElements) const T * const aIn, __out_ecount(cElements) T* const aOut, const size_t cElements, const T fRunningSumIn = 0)
{
T fRunningSum = fRunningSumIn;
for (size_t iOnElement = 0; iOnElement < cElements; iOnElement++)
{
aOut[iOnElement] = (fRunningSum += aIn[iOnElement]);
}
return fRunningSum;
}
template<const unsigned char nElementsToShift>
__forceinline __m128 _mm_slli_ps(__m128 m)
{
return _mm_castsi128_ps(_mm_slli_si128(_mm_castps_si128(m), 4 * nElementsToShift));
}
__forceinline __m128 SumRegister(__m128 mIn)
{
__m128 mAddShift = _mm_add_ps(mIn, _mm_slli_ps<1>(mIn));
return _mm_add_ps(mAddShift, _mm_slli_ps<2>(mAddShift));
}
float CumulativeSum_SSE(const float * const aIn, float * const aOut, size_t cElements, float fRunningSum = 0)
{
size_t cOnElement = cElements & 3;
fRunningSum = SumArray(aIn, aOut, cOnElement, fRunningSum);
__m128 mLeftSum = _mm_set1_ps(fRunningSum);
if (cElements & 4)
{
__m128 mIn = _mm_loadu_ps(aIn + cOnElement);
__m128 mOut = _mm_add_ps(mLeftSum, SumRegister(mIn));
_mm_storeu_ps(aOut + cOnElement, mOut);
mLeftSum = _mm_shuffle_ps(mOut, mOut, _MM_SHUFFLE(3, 3, 3, 3));
cOnElement += 4;
}
while (cOnElement<cElements)
{
__m128 mInLo = _mm_loadu_ps(aIn + cOnElement);
__m128 mInHi = _mm_loadu_ps(aIn + cOnElement + 4);
__m128 mSummedInLo = SumRegister(mInLo);
__m128 mSummedInHi = SumRegister(mInHi);
__m128 mOutLo = _mm_add_ps(mLeftSum, mSummedInLo);
_mm_storeu_ps(aOut + cOnElement, mOutLo);
mLeftSum = _mm_shuffle_ps(mOutLo, mOutLo, _MM_SHUFFLE(3, 3, 3, 3));
__m128 mOutHi = _mm_add_ps(mLeftSum, mSummedInHi);
_mm_storeu_ps(aOut + cOnElement + 4, mOutHi);
mLeftSum = _mm_shuffle_ps(mOutHi, mOutHi, _MM_SHUFFLE(3, 3, 3, 3));
cOnElement += 8;
}
return _mm_cvtss_f32(mLeftSum);
}
And then the 2-dimensional summation will look pretty similar:
void BoxFilterPreCalc_SSE(const float * const aIn, float * const aOut, const size_t cHorizontalElements, const size_t cVerticalElements, const ptrdiff_t verticalStrideIn, const ptrdiff_t verticalStrideOut)
{
if (!cVerticalElements)
{
return;
}
CumulativeSum_SSE(aIn, aOut, cHorizontalElements, 0);
size_t cRowsRemaining = cVerticalElements - 1;
const float *pStartOutPrevLine = aOut;
float *pStartOutCurLine = AddBytesToPointer(aOut, verticalStrideOut);
const float *pStartInCurLine = AddBytesToPointer(aIn, verticalStrideIn);
while (cRowsRemaining-- > 0)
{
float fLeftSum = 0;
size_t iOnElement = 0;
size_t cElementsRemaining = cHorizontalElements;
while (cElementsRemaining & 3)
{
cElementsRemaining--;
pStartOutCurLine[iOnElement] = pStartOutPrevLine[iOnElement]+(fLeftSum += pStartInCurLine[iOnElement]);
iOnElement++;
}
__m128 mLeftSum = _mm_set1_ps(fLeftSum);
if (cElementsRemaining & 4)
{
cElementsRemaining -= 4;
__m128 mInLo = _mm_loadu_ps(pStartInCurLine + iOnElement);
__m128 mPrevOutLo = _mm_loadu_ps(pStartOutPrevLine + iOnElement);
__m128 mSummedInLo = SumRegister(mInLo);
__m128 mLeftSumOutLo = _mm_add_ps(mLeftSum, mSummedInLo);
__m128 mOutLo = _mm_add_ps(mLeftSumOutLo, mPrevOutLo);
_mm_storeu_ps(pStartOutCurLine + iOnElement, mOutLo);
mLeftSum = _mm_shuffle_ps(mLeftSumOutLo, mLeftSumOutLo, _MM_SHUFFLE(3, 3, 3, 3));
iOnElement += 4;
}
while (cElementsRemaining > 0)
{
cElementsRemaining -= 8;
__m128 mInLo = _mm_loadu_ps(pStartInCurLine + iOnElement);
__m128 mInHi = _mm_loadu_ps(pStartInCurLine + iOnElement + 4);
__m128 mPrevOutLo = _mm_loadu_ps(pStartOutPrevLine + iOnElement);
__m128 mPrevOutHi = _mm_loadu_ps(pStartOutPrevLine + iOnElement+4);
__m128 mSummedInLo = SumRegister(mInLo);
__m128 mSummedInHi = SumRegister(mInHi);
__m128 mLeftSumOutLo = _mm_add_ps(mLeftSum, mSummedInLo);
__m128 mOutLo = _mm_add_ps(mLeftSumOutLo, mPrevOutLo);
_mm_storeu_ps(pStartOutCurLine + iOnElement, mOutLo);
__m128 mLeftSum = _mm_shuffle_ps(mLeftSumOutLo, mLeftSumOutLo, _MM_SHUFFLE(3, 3, 3, 3));
__m128 mLeftSumOutHi = _mm_add_ps(mLeftSum, mSummedInHi);
__m128 mOutHi = _mm_add_ps(mLeftSumOutHi, mPrevOutHi);
_mm_storeu_ps(pStartOutCurLine + iOnElement + 4, mOutHi);
mLeftSum = _mm_shuffle_ps(mLeftSumOutHi, mLeftSumOutHi, _MM_SHUFFLE(3, 3, 3, 3));
iOnElement += 8;
}
pStartOutPrevLine = pStartOutCurLine;
pStartOutCurLine = AddBytesToPointer(pStartOutCurLine, verticalStrideOut);
pStartInCurLine = AddBytesToPointer(pStartInCurLine, verticalStrideIn);
}
}
For some similar opterations we will actually legitimately need the increased accuracy of doubles. That's coming soon.
Sunday, May 7, 2017
Levenshtein distance using SSSE3 and SSE41
Levenshtein distance is a measure of how close two strings are to each other. The distance is the count of additions, deletions, and substitutions necessary to transform one string into another.
The following is a fairly faithful translation from the code in the Wikipedia article into C++.
template <typename T>
void swap(T & a, T& b)
{
T temp = a;
a = b;
b = temp;
}
size_t Levenshtein_distance_ANSI(LPCWSTR s, LPCWSTR t)
{
size_t lenS = wcslen(s);
size_t lenT = wcslen(t);
if ((0 == lenS) || (0== lenT) || (0==wcscmp(s,t)))
{
return 0;
}
// create two work vectors of integer distances
int *v0 = new int[lenT+1];
int *v1 = new int[lenT+1];
// initialize v0 (the previous row of distances)
// this row is A[0][i]: edit distance for an empty s
// the distance is just the number of characters to delete from t
for (size_t i = 0; i <= lenT; i++)
{
v0[i] = i;
}
for (size_t i = 0; i <lenS; i++)
{
// calculate v1 (current row distances) from the previous row v0
// first element of v1 is A[i+1][0]
// edit distance is delete (i+1) chars from s to match empty t
v1[0] = i + 1;
// use formula to fill in the rest of the row
for (int j = 0; j <lenT; j++)
{
int cost = (s[i] != t[j]);
int right = v1[j] + 1;
int down = v0[j + 1] + 1;
int diag = v0[j] + cost;
v1[j + 1] = min(min(right, down), diag);
}
// swap v1 (current row) to v0 (previous row) for next iteration
swap(v0, v1);
}
size_t retVal = v0[lenT];
delete[] v0;
delete[] v1;
return retVal;
}
I have made one minor change. The code above swaps the pointers instead of recopying from the destination row back into the source row.
size_t Levenshtein_distance_SSE42(LPCWSTR s, LPCWSTR t)
{
size_t lenS = wcslen(s);
size_t lenT = wcslen(t);
if ((0 == lenS) || (0 == lenT) || (0 == wcscmp(s, t)))
{
return 0;
}
// create two work vectors of integer distances
int *v0 = new int[lenT + 1];
int *v1 = new int[lenT + 1];
// initialize v0 (the previous row of distances)
// this row is A[0][i]: edit distance for an empty s
// the distance is just the number of characters to delete from t
for (size_t i = 0; i <= lenT; i++)
{
v0[i] = i;
}
const __m128i mOne = _mm_set1_epi32(1);
const __m128i mTwo = _mm_set1_epi32(2);
const __m128i mFour = _mm_set1_epi32(4);
for (size_t i = 0; i <lenS; i++)
{
// calculate v1 (current row distances) from the previous row v0
// first element of v1 is A[i+1][0]
// edit distance is delete (i+1) chars from s to match empty t
v1[0] = i + 1;
// use formula to fill in the rest of the
// first handle the first elements so that the remainder is a multiple of 4
size_t j = 0;
while ((lenT - j) &3)
{
int cost = (s[i] != t[j]);
int right = v1[j] + 1;
int diag = v0[j] + cost;
j++;
int down = v0[j] + 1;
v1[j] = min(min(right, down), diag);
}
// Any left over at this point can be handled in blocks of four elements.
if (j<lenT)
{
__m128i msi = _mm_set1_epi16(s[i]);
__m128i mPrevBest = _mm_set1_epi32(v1[j]);
do {
__m128i v0lo = _mm_loadu_si128((__m128i *)&v0[j]);
__m128i v0loOffset = _mm_loadu_si128((__m128i *)&v0[j + 1]);
__m128i mtj = _mm_set1_epi64x(*(__int64 *)&t[j]);
__m128i mstCmp = _mm_cmpeq_epi16(msi, mtj);
__m128i mCost = _mm_add_epi32(mOne, _mm_unpacklo_epi16(mstCmp, mstCmp));
__m128i mDiag = _mm_add_epi32(v0lo, mCost);
__m128i mDown = _mm_add_epi32(mOne, v0loOffset);
__m128i mMinDiagDown = _mm_min_epi32(mDiag, mDown);
__m128i mRightOne = _mm_min_epi32(mMinDiagDown, _mm_add_epi32(mOne, _mm_alignr_epi8(mMinDiagDown, mPrevBest, 12)));
__m128i mRightTwo = _mm_add_epi32(mTwo, _mm_alignr_epi8(mRightOne, mPrevBest, 8));
__m128i mRightFour = _mm_add_epi32(mFour, mPrevBest);
__m128i mBest = _mm_min_epi32(mRightOne, _mm_min_epi32(mRightFour, mRightTwo));
mPrevBest = mBest;
_mm_storeu_si128((__m128i *)&v1[j + 1], mBest);
j += 4;
} while (j<lenT);
}
// swap v1 (current row) to v0 (previous row) for next iteration
swap(v0, v1);
}
size_t retVal = v0[lenT];
delete[] v0;
delete[] v1;
return retVal;
}
This is a pretty faithful reimplementation of the first version. It takes about 1/3 the wall-clock time of the ansi implementation. Note that there are two reads from memory per inner loop iteration. This can be addressed by reading one group of four ahead.
The horizontal minimums are performed by doing a min against the block shifted left one element, then by two elements, then by four elements, each plus a constant.
Other implementation I see on the internet use a different algorithm based on calculation along the diagonal. A bit harder to understand. But we will revisit that later.
The following is a fairly faithful translation from the code in the Wikipedia article into C++.
template <typename T>
void swap(T & a, T& b)
{
T temp = a;
a = b;
b = temp;
}
size_t Levenshtein_distance_ANSI(LPCWSTR s, LPCWSTR t)
{
size_t lenS = wcslen(s);
size_t lenT = wcslen(t);
if ((0 == lenS) || (0== lenT) || (0==wcscmp(s,t)))
{
return 0;
}
// create two work vectors of integer distances
int *v0 = new int[lenT+1];
int *v1 = new int[lenT+1];
// initialize v0 (the previous row of distances)
// this row is A[0][i]: edit distance for an empty s
// the distance is just the number of characters to delete from t
for (size_t i = 0; i <= lenT; i++)
{
v0[i] = i;
}
for (size_t i = 0; i <lenS; i++)
{
// calculate v1 (current row distances) from the previous row v0
// first element of v1 is A[i+1][0]
// edit distance is delete (i+1) chars from s to match empty t
v1[0] = i + 1;
// use formula to fill in the rest of the row
for (int j = 0; j <lenT; j++)
{
int cost = (s[i] != t[j]);
int right = v1[j] + 1;
int down = v0[j + 1] + 1;
int diag = v0[j] + cost;
v1[j + 1] = min(min(right, down), diag);
}
// swap v1 (current row) to v0 (previous row) for next iteration
swap(v0, v1);
}
size_t retVal = v0[lenT];
delete[] v0;
delete[] v1;
return retVal;
}
I have made one minor change. The code above swaps the pointers instead of recopying from the destination row back into the source row.
size_t Levenshtein_distance_SSE42(LPCWSTR s, LPCWSTR t)
{
size_t lenS = wcslen(s);
size_t lenT = wcslen(t);
if ((0 == lenS) || (0 == lenT) || (0 == wcscmp(s, t)))
{
return 0;
}
// create two work vectors of integer distances
int *v0 = new int[lenT + 1];
int *v1 = new int[lenT + 1];
// initialize v0 (the previous row of distances)
// this row is A[0][i]: edit distance for an empty s
// the distance is just the number of characters to delete from t
for (size_t i = 0; i <= lenT; i++)
{
v0[i] = i;
}
const __m128i mOne = _mm_set1_epi32(1);
const __m128i mTwo = _mm_set1_epi32(2);
const __m128i mFour = _mm_set1_epi32(4);
for (size_t i = 0; i <lenS; i++)
{
// calculate v1 (current row distances) from the previous row v0
// first element of v1 is A[i+1][0]
// edit distance is delete (i+1) chars from s to match empty t
v1[0] = i + 1;
// use formula to fill in the rest of the
// first handle the first elements so that the remainder is a multiple of 4
size_t j = 0;
while ((lenT - j) &3)
{
int cost = (s[i] != t[j]);
int right = v1[j] + 1;
int diag = v0[j] + cost;
j++;
int down = v0[j] + 1;
v1[j] = min(min(right, down), diag);
}
// Any left over at this point can be handled in blocks of four elements.
if (j<lenT)
{
__m128i msi = _mm_set1_epi16(s[i]);
__m128i mPrevBest = _mm_set1_epi32(v1[j]);
do {
__m128i v0lo = _mm_loadu_si128((__m128i *)&v0[j]);
__m128i v0loOffset = _mm_loadu_si128((__m128i *)&v0[j + 1]);
__m128i mtj = _mm_set1_epi64x(*(__int64 *)&t[j]);
__m128i mstCmp = _mm_cmpeq_epi16(msi, mtj);
__m128i mCost = _mm_add_epi32(mOne, _mm_unpacklo_epi16(mstCmp, mstCmp));
__m128i mDiag = _mm_add_epi32(v0lo, mCost);
__m128i mDown = _mm_add_epi32(mOne, v0loOffset);
__m128i mMinDiagDown = _mm_min_epi32(mDiag, mDown);
__m128i mRightOne = _mm_min_epi32(mMinDiagDown, _mm_add_epi32(mOne, _mm_alignr_epi8(mMinDiagDown, mPrevBest, 12)));
__m128i mRightTwo = _mm_add_epi32(mTwo, _mm_alignr_epi8(mRightOne, mPrevBest, 8));
__m128i mRightFour = _mm_add_epi32(mFour, mPrevBest);
__m128i mBest = _mm_min_epi32(mRightOne, _mm_min_epi32(mRightFour, mRightTwo));
mPrevBest = mBest;
_mm_storeu_si128((__m128i *)&v1[j + 1], mBest);
j += 4;
} while (j<lenT);
}
// swap v1 (current row) to v0 (previous row) for next iteration
swap(v0, v1);
}
size_t retVal = v0[lenT];
delete[] v0;
delete[] v1;
return retVal;
}
This is a pretty faithful reimplementation of the first version. It takes about 1/3 the wall-clock time of the ansi implementation. Note that there are two reads from memory per inner loop iteration. This can be addressed by reading one group of four ahead.
The horizontal minimums are performed by doing a min against the block shifted left one element, then by two elements, then by four elements, each plus a constant.
Other implementation I see on the internet use a different algorithm based on calculation along the diagonal. A bit harder to understand. But we will revisit that later.
Sunday, April 30, 2017
Distance between adjacent points in a polyline using SSE3
We will need this a little bit later to talk about splines. Spline approximation is usually done using an iterative process. The parametric variable is usually given a starting position based on the distance between the points in the polyline.
So it is a real-world problem to create an array of the distance between adjacent points in a polyline.
typedef struct
{
float x;
float y;
} Pointf2d;
__forceinline float DistanceBetweenPoints(const Pointf2d & aXY, const Pointf2d & bXY)
{
return _hypotf(aXY.x - bXY.x, aXY.y - bXY.y);
}
void distanceBetween2dPoints_ANSI(const size_t cPoints, __in_ecount(cPoints) const Pointf2d* const paxy, __in_ecount(cPoints) const Pointf2d * const pbxy, __out_ecount(cPoints) float * const pDists)
{
size_t onPoint = cPoints;
while (onPoint-- > 0)
{
pDists[onPoint] = DistanceBetweenPoints(paxy[onPoint], pbxy[onPoint]);
}
}
void lengthOfPolylineSegments_ANSI(const size_t cPoints, __in_ecount(cPoints) const Pointf2d* const paxy, __out_ecount(cPoints-1) float * const pLengths)
{
if (cPoints > 0)
{
distanceBetween2dPoints_ANSI(cPoints - 1, &paxy[0], &paxy[1], pLengths);
}
}
So it is a real-world problem to create an array of the distance between adjacent points in a polyline.
typedef struct
{
float x;
float y;
} Pointf2d;
{
return _hypotf(aXY.x - bXY.x, aXY.y - bXY.y);
}
void distanceBetween2dPoints_ANSI(const size_t cPoints, __in_ecount(cPoints) const Pointf2d* const paxy, __in_ecount(cPoints) const Pointf2d * const pbxy, __out_ecount(cPoints) float * const pDists)
{
size_t onPoint = cPoints;
while (onPoint-- > 0)
{
pDists[onPoint] = DistanceBetweenPoints(paxy[onPoint], pbxy[onPoint]);
}
}
void lengthOfPolylineSegments_ANSI(const size_t cPoints, __in_ecount(cPoints) const Pointf2d* const paxy, __out_ecount(cPoints-1) float * const pLengths)
{
if (cPoints > 0)
{
distanceBetween2dPoints_ANSI(cPoints - 1, &paxy[0], &paxy[1], pLengths);
}
}
This translates pretty easily into SSE. It does rely on a horizontal add, which I have left using the SSE3 intrinsic.
void distanceBetween2dPoints_SSE3(const size_t cPoints, __in_ecount(cPoints) const Pointf2d* const paxy, __in_ecount(cPoints) const Pointf2d * const pbxy, __out_ecount(cPoints) float * const pDists)
{
size_t onPoint = cPoints;
while (onPoint & 3)
{
onPoint--;
pDists[onPoint] = DistanceBetweenPoints(paxy[onPoint], pbxy[onPoint]);
}
while (onPoint > 0)
{
onPoint -= 4;
__m128 mAXYhi = _mm_loadu_ps((float *)&paxy[onPoint+2]);
__m128 mBXYhi = _mm_loadu_ps((float *)&pbxy[onPoint+2]);
__m128 mAXYlo = _mm_loadu_ps((float *)&paxy[onPoint]);
__m128 mBXYlo = _mm_loadu_ps((float *)&pbxy[onPoint]);
__m128 mDiffHi = _mm_sub_ps(mAXYhi, mBXYhi);
__m128 mDiffLo = _mm_sub_ps(mAXYlo, mBXYlo);
__m128 mDiffSqrHi = _mm_mul_ps(mDiffHi, mDiffHi);
__m128 mDiffSqrLo = _mm_mul_ps(mDiffLo, mDiffLo);
__m128 mSumDiffSqr = _mm_hadd_ps(mDiffSqrLo, mDiffSqrHi);
__m128 mSqrtSumDiffSqr = _mm_sqrt_ps(mSumDiffSqr);
_mm_storeu_ps(&pDists[onPoint], mSqrtSumDiffSqr);
}
}
void lengthOfPolylineSegments_SSE3(const size_t cPoints, __in_ecount(cPoints) const Pointf2d* const paxy, __out_ecount(cPoints-1) float * const pLengths)
{
if (cPoints > 0)
{
distanceBetween2dPoints_SSE(cPoints - 1, &paxy[0], &paxy[1], pLengths);
}
}
This code can be more efficient. Using the same variable twice for use in the SSE3 implementation makes for easy to understand code. But we can do a little better using the _mm_alignr_epi8 intrinsic, and will see that soon.
Subscribe to:
Comments (Atom)