evaluating a 2d cubic spline using SSE. subdividing a 2d cubic spline using SSE.

I really like Bezier cubic splines.  Unfortunately, this post will assume some understanding of them, and will not make as much sense without that understanding.  If you don't have problems with these curves, this post may not be quite as accessible.  I will ask you to assume that these are real problems that real people have with these curves.

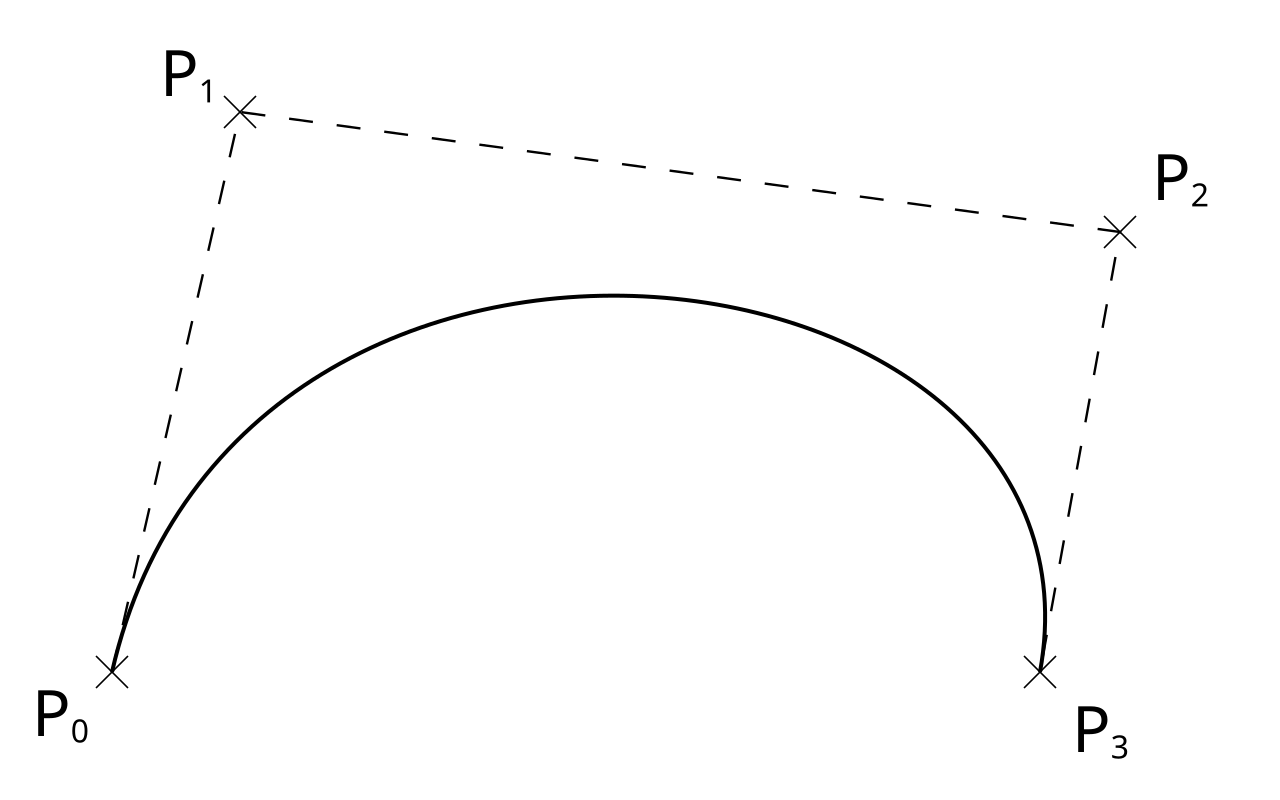
Cubic splines are pretty.  A 2d curve is described with 4 points as diagramed above.  The curve starts at P0 and ends at P3.  At P0 the curve starts by going in the direction of P1.  At P3 the curve ends while going in the direction away from P2.  And many other useful properties.

Sometimes we will end up wanting to evaluate the curve along its' path.  We construct a parametric representation and evaluate as the parameter t varies from 0 to 1.  Each of the dimensions will be evaluated as a cubic polynomial in t.  We can construct the polynomial and evaluate directly. Or...

There's another way to evaluate cubic splines, called De Casteljau's algorithm.  This works nicely with SSE.

It is a recursive process, generating a spline of lower order at each level.  The recursion is unrolled in the implementation below:

void AffineInterpolate(const __m128 &mP0123, const __m128 &mT, __m128 &mQ012)
{
    __m128 mP0123t = _mm_mul_ps(mP0123, mT);
    __m128 mP0123omt = _mm_sub_ps(mP0123, mP0123t);
    __m128 mP1233t = _mm_shuffle_ps(mP0123t, mP0123t, _MM_SHUFFLE(3, 3, 2, 1));
    mQ012 = _mm_add_ps(mP0123omt, mP1233t);
}
float evaluate1DCubicSplineAt(const __m128 &mP0123, const __m128 &mT)
{
    __m128 mQ012;
    __m128 mR01;
    __m128 mS0;
    AffineInterpolate(mP0123, mT, mQ012);
    AffineInterpolate(mQ012, mT, mR01);
    AffineInterpolate(mR01, mT, mS0);
    return _mm_cvtss_f32(mS0);
}
void evaluate2DCubicSplineAt(__in_ecount(8) const float *P0123xy, const float t, __out_ecount(2) float * const pResultXY)
{
    const __m128 mP01 = _mm_loadu_ps(&P0123xy[0]);
    const __m128 mP23 = _mm_loadu_ps(&P0123xy[4]);
    __m128 mT = _mm_set1_ps(t);
    __m128 mP0123x = _mm_shuffle_ps(mP01, mP23, _MM_SHUFFLE(2, 0, 2, 0));
    __m128 mP0123y = _mm_shuffle_ps(mP01, mP23, _MM_SHUFFLE(3, 1, 3, 1));
    pResultXY[0] = evaluate1DCubicSplineAt(mP0123x, mT);
    pResultXY[1] = evaluate1DCubicSplineAt(mP0123y, mT);
}

This splits the 2d control points into two sets of 1d control points.  These are evaluated separately.

The cubic Bezier curve can be split losslessly into two separate curves along its length.  All of the control points necessary for this are in fact present in the intermediates of evaluate1DCubicSplineAt.  So let's extract them.

void split1DCubicSplineAt(const __m128 &mP0123, const __m128 &mT, __m128 & leftOut, __m128 &rightOut)
{
    __m128 mQ012;
    __m128 mR01;
    __m128 mS0;
    AffineInterpolate(mP0123, mT, mQ012);
    AffineInterpolate(mQ012, mT, mR01);
    AffineInterpolate(mR01, mT, mS0);
    __m128 mPQ = _mm_shuffle_ps(mP0123, mQ012, _MM_SHUFFLE(2, 0, 3, 0));
    __m128 mRS = _mm_shuffle_ps(mR01, mS0, _MM_SHUFFLE(0, 0, 1, 0));
    leftOut = _mm_shuffle_ps(mPQ, mRS, _MM_SHUFFLE(2, 0, 2, 0));
    rightOut = _mm_shuffle_ps(mRS, mPQ, _MM_SHUFFLE(1, 3, 1, 3));
}
void split2DCubicSplineAt(__in_ecount(8) const float *P0123xy, const float t, __out_ecount(16) float * const pSplitCurvesXY)
{
    const __m128 mP01 = _mm_loadu_ps(&P0123xy[0]);
    const __m128 mP23 = _mm_loadu_ps(&P0123xy[4]);
    __m128 mT = _mm_set1_ps(t);
    __m128 mP0123x = _mm_shuffle_ps(mP01, mP23, _MM_SHUFFLE(2, 0, 2, 0));
    __m128 mP0123y = _mm_shuffle_ps(mP01, mP23, _MM_SHUFFLE(3, 1, 3, 1));
    __m128 mLeftX, mLeftY, mRightX, mRightY;
    split1DCubicSplineAt(mP0123x, mT, mLeftX, mRightX);
    split1DCubicSplineAt(mP0123y, mT, mLeftY, mRightY);
    __m128 mLeftXyLo = _mm_unpacklo_ps(mLeftX, mLeftY);
    __m128 mLeftXyHi = _mm_unpackhi_ps(mLeftX, mLeftY);
    __m128 mRightXyLo = _mm_unpacklo_ps(mRightX, mRightY);
    __m128 mRightXyHi = _mm_unpackhi_ps(mRightX, mRightY);
    _mm_storeu_ps(&pSplitCurvesXY[0], mLeftXyLo);
    _mm_storeu_ps(&pSplitCurvesXY[4], mLeftXyHi);
    _mm_storeu_ps(&pSplitCurvesXY[8], mRightXyLo);
    _mm_storeu_ps(&pSplitCurvesXY[12], mRightXyHi);
}

This yields two separate Bezier curves, both output to pSplitCurvesXY.  The last point of the first of the Bezier curves is the evaluation at t.  This is exactly the same as the first point of the second Bezier curve.  In SVG paths this duplicated point would be omitted. 

This requires 3 multiplies, 3 adds, and 3 subtractions for each of the 1d evaluation or subdivision.  And a bunch of very fast shuffles.  The final multiply of each 1d could be combined with each other.  But it doesn't seem worth the added complexity.

This compiles to x86 assembly without register spills.