Transposing a 16x16 bit matrix using SSE2 and AVX2.

Building on the 16x8 matrix transpose from a previous post, it's pretty easy to make a 16x16 matrix transpose.

void BitMatrixTranspose_16x16_SSE(const __m128i &aIn, const __m128i &bIn, __m128i & cOut, __m128i &dOut)
{

    __m128i mLeft = BitMatrixTranspose_16x8_SSE(aIn);
    __m128i mRight = BitMatrixTranspose_16x8_SSE(bIn);
    cOut = _mm_unpacklo_epi8(mLeft, mRight);
    dOut = _mm_unpackhi_epi8(mLeft, mRight);
}

Most new machines support AVX and AVX2 these days.

__m256i unpack8_AVX2(const __m256i&xIn)
{
    __m256i mRet = _mm256_unpacklo_epi8(xIn, _mm256_shuffle_epi32(xIn, _MM_SHUFFLE(3, 2, 3, 2)));
    return mRet;
}

__m256i repack8_AVX2(const __m256i&xIn)
{
    return unpack8_SSE(unpack8_SSE(unpack8_SSE(xIn)));
}

__m256i BitMatrixTranspose_8x8_AVX2(const __m256i &xIn)
{
    const __m256i c1 = _mm256_set1_epi64x(0xAA55AA55AA55AA55LL);
    const __m256i c2 = _mm256_set1_epi64x(0x00AA00AA00AA00AALL);
    const __m256i c3 = _mm256_set1_epi64x(0xCCCC3333CCCC3333LL);
    const __m256i c4 = _mm256_set1_epi64x(0x0000CCCC0000CCCCLL);
    const __m256i c5 = _mm256_set1_epi64x(0xF0F0F0F00F0F0F0FLL);
    const __m256i c6 = _mm256_set1_epi64x(0x00000000F0F0F0F0LL);

    const __m256i x1 = _mm256_or_si256(_mm256_and_si256(xIn, c1), _mm256_or_si256(_mm256_slli_epi64(_mm256_and_si256(xIn, c2), 7), _mm256_and_si256(_mm256_srli_epi64(xIn, 7), c2)));
    const __m256i x2 = _mm256_or_si256(_mm256_and_si256(x1, c3), _mm256_or_si256(_mm256_slli_epi64(_mm256_and_si256(x1, c4), 14), _mm256_and_si256(_mm256_srli_epi64(x1, 14), c4)));
    const __m256i x3 = _mm256_or_si256(_mm256_and_si256(x2, c5), _mm256_or_si256(_mm256_slli_epi64(_mm256_and_si256(x2, c6), 28), _mm256_and_si256(_mm256_srli_epi64(x2, 28), c6)));

    return x3;
}

__m256i BitMatrixTranspose_16x16_AVX2(const __m256i &xIn)
{
    __m256i mUnshuffle = repack8_AVX2(xIn);
    __m256i mSmallTranspose= BitMatrixTranspose_8x8_AVX2(mUnshuffle);
    __m256i mRet = unpack8_across_lanes_AVX2(mSmallTranspose);
    return mRet;
}

This follows the same shuffle pattern used in SSE2.  But the shuffle could be rewritten and simplified using the arbitrary byte shuffle instruction:

__m256i repack8_AVX2(const __m256i&xIn)
{
    const __m256i xShuffleConst = _mm256_set_epi64x(0x0f0d0b0907050301LL, 0x0e0c0a0806040200LL, 0x0f0d0b0907050301LL, 0x0e0c0a0806040200LL);
    __m256i mRet = _mm256_shuffle_epi8(xIn, xShuffleConst);
    return mRet;
}

I would normally declare the above 256bit constant static.  But it appears that MSVC doesn't handle static __m256i variables as well as it does static __m128i.

Transposing a bit matrix using SSE2

In order to make a error correcting code more resilient to burst errors, it's not uncommon to interleave bits from multiple encoded words.  

Intuitively we can think of making a 2d matrix with each row being a separate codeword.  Interleaving the bits is then just taking the transpose of the bit matrix.

The book "Hacker's Delight" has an ansi algorithm for transposing a 8x8 bit matrix (64 bits total):

unsigned __int64 transpose8(unsigned __int64 x)
{
    x = (x & 0xAA55AA55AA55AA55LL) | ((x & 0x00AA00AA00AA00AALL) << 7) | ((x >> 7) & 0x00AA00AA00AA00AALL);
    x = (x & 0xCCCC3333CCCC3333LL) | ((x & 0x0000CCCC0000CCCCLL) << 14) | ((x >> 14) & 0x0000CCCC0000CCCCLL);
    x = (x & 0xF0F0F0F00F0F0F0FLL) | ((x & 0x00000000F0F0F0F0LL) << 28) | ((x >> 28) & 0x00000000F0F0F0F0LL);
    return x;
}

This can be directly translated into SSE code, which will transpose two separate 8x8 matrices at the same time:

__m128i BitMatrixTranspose_8x8_SSE(const __m128i &xIn)
{
    const __m128i c1 = _mm_set1_epi64x(0xAA55AA55AA55AA55LL);
    const __m128i c2 = _mm_set1_epi64x(0x00AA00AA00AA00AALL);
    const __m128i c3 = _mm_set1_epi64x(0xCCCC3333CCCC3333LL);
    const __m128i c4 = _mm_set1_epi64x(0x0000CCCC0000CCCCLL);
    const __m128i c5 = _mm_set1_epi64x(0xF0F0F0F00F0F0F0FLL);
    const __m128i c6 = _mm_set1_epi64x(0x00000000F0F0F0F0LL);

    const __m128i x1 = _mm_or_si128(_mm_and_si128(xIn, c1), _mm_or_si128(_mm_slli_epi64(_mm_and_si128(xIn, c2), 7), _mm_and_si128(_mm_srli_epi64(xIn, 7), c2)));
    const __m128i x2 = _mm_or_si128(_mm_and_si128(x1, c3), _mm_or_si128(_mm_slli_epi64(_mm_and_si128(x1, c4), 14), _mm_and_si128(_mm_srli_epi64(x1, 14), c4)));
    const __m128i x3 = _mm_or_si128(_mm_and_si128(x2, c5), _mm_or_si128(_mm_slli_epi64(_mm_and_si128(x2, c6), 28), _mm_and_si128(_mm_srli_epi64(x2, 28), c6)));

    return x3;
}

A transpose operation on a square matrix is self inverse.  So the above function is self inverse.

This can then be extended to take the transpose of an 8x16 matrix and a 16x8 matrix (inverse functions of each other).

__m128i unpack8_SSE(const __m128i&xIn)
{
    __m128i mRet = _mm_unpacklo_epi8(xIn, _mm_shuffle_epi32(xIn, _MM_SHUFFLE(3, 2, 3, 2)));
    return mRet;
}

__m128i repack8_SSE(const __m128i&xIn)
{
    return unpack8_SSE(unpack8_SSE(unpack8_SSE(xIn)));
}

__m128i BitMatrixTranspose_8x16_SSE(const __m128i &xIn)
{
    __m128i mTransposedHalves = BitMatrixTranspose_8x8_SSE(xIn);
    __m128i mRet = unpack8_SSE(mTransposedHalves);
    return mRet;
}

__m128i BitMatrixTranspose_16x8_SSE(const __m128i &xIn)
{
    __m128i mUnshuffle = repack8_SSE(xIn);
    __m128i mRet = BitMatrixTranspose_8x8_SSE(mUnshuffle);
    return mRet;
}

It's also worth noting that unpack8_SSE and repack8_SSE are inverses of each other.
This could be simplified using the _mm_shuffle_epi8 instruction.  But that's a different problem.

A bitonic sorting network for 16 float in SSE2

A while back I gave source code for a 8 float bitonic sorting network.
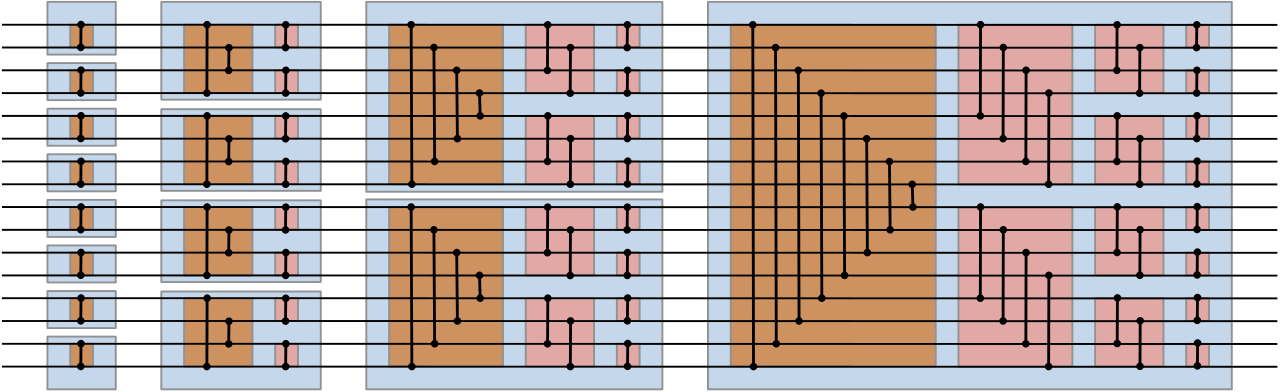
Bitonic sorting networks can be recursively expanded to larger sorting networks.  So we have the main building block for a 16 float bitonic sorting network.  The two halves are sorted, then merged together.

Here's the previously seen 8 float network.

void BitonicSortingNetwork8_SSE2(const __m128 &a, const __m128 &b, __m128 &aOut, __m128 &bOut)
{
    __m128 a1 = a;
    __m128 b1 = b;
    __m128 a1Min = _mm_min_ps(a1, b1); // 1357
    __m128 b1Max = _mm_max_ps(a1, b1); // 2468
    __m128 a2 = a1Min; // 1357
    __m128 b2 = _mm_shuffle_ps(b1Max, b1Max, _MM_SHUFFLE(2, 3, 0, 1)); // 4286
    __m128 a2Min = _mm_min_ps(a2, b2); // 1256
    __m128 b2Max = _mm_max_ps(a2, b2); // 4387
    __m128 a3 = _mm_shuffle_ps(a2Min, b2Max, _MM_SHUFFLE(3, 1, 2, 0)); // 1537
    __m128 b3 = _mm_shuffle_ps(a2Min, b2Max, _MM_SHUFFLE(2, 0, 3, 1)); // 2648
    __m128 a3Min = _mm_min_ps(a3, b3); // 1537
    __m128 b3Max = _mm_max_ps(a3, b3); // 2648
    __m128 a4 = a3Min; // 1537
    __m128 b4 = _mm_shuffle_ps(b3Max, b3Max, _MM_SHUFFLE(0, 1, 2, 3)); // 8462
    __m128 a4Min = _mm_min_ps(a4, b4); // 1432
    __m128 b4Max = _mm_max_ps(a4, b4); // 8567
    __m128 a5 = _mm_unpacklo_ps(a4Min, b4Max); // 1845
    __m128 b5 = _mm_unpackhi_ps(a4Min, b4Max); // 3627
    __m128 a5Min = _mm_min_ps(a5, b5); // 1625
    __m128 b5Max = _mm_max_ps(a5, b5); // 3847
    __m128 a6 = _mm_unpacklo_ps(a5Min, b5Max); // 1368
    __m128 b6 = _mm_unpackhi_ps(a5Min, b5Max); // 2457
    __m128 a6Min = _mm_min_ps(a6, b6); // 1357
    __m128 b6Max = _mm_max_ps(a6, b6); // 2468
    aOut = _mm_unpacklo_ps(a6Min, b6Max); // 1234
    bOut = _mm_unpackhi_ps(a6Min, b6Max); // 5678
}

This is the topLeft group of the 16 float network.  It is also the bottomLeft group of the 16 float network.

This leaves the right half.  The last 3 sets of comparisons look like the last 3 comparisons of the 8 float network.

void UpperHalfRightHalfBitonicSorter_SSE2(const __m128 &aIn, const __m128 &bIn, __m128 &aOut, __m128 &bOut)
{
    __m128 a1 = aIn; // 1234
    __m128 b1 = bIn; // 5678
    __m128 a1Min = _mm_min_ps(a1, b1); // 1234
    __m128 b1Max = _mm_max_ps(a1, b1); // 5678
    __m128 a2 = _mm_unpacklo_ps(a1Min, b1Max); // 1526
    __m128 b2 = _mm_unpackhi_ps(a1Min, b1Max); // 3748
    __m128 a2Min = _mm_min_ps(a2, b2); // 1526
    __m128 b2Max = _mm_max_ps(a2, b2); // 3748
    __m128 a3 = _mm_unpacklo_ps(a2Min, b2Max); // 1357
    __m128 b3 = _mm_unpackhi_ps(a2Min, b2Max); // 2468
    __m128 a3Min = _mm_min_ps(a3, b3); // 1357
    __m128 b3Max = _mm_max_ps(a3, b3); // 2468
    aOut = _mm_unpacklo_ps(a3Min, b3Max); // 1234
    bOut = _mm_unpackhi_ps(a3Min, b3Max); // 5678
}

And then there's the large group of 16 comparisons in the very center.
And it all gets put together.

void BitonicSortingNetwork16_SSE2(const __m128 &aIn, const __m128 &bIn, const __m128 &cIn, const __m128 &dIn,

    __m128 &aOut, __m128 &bOut, __m128 &cOut, __m128 &dOut

)

{

    __m128 a1 = aIn, b1 = bIn, c1 = cIn, d1 = dIn;

    __m128 a2, b2, c2, d2;

    BitonicSortingNetwork8_SSE2(a1, b1, a2, b2);

    BitonicSortingNetwork8_SSE2(c1, d1, c2, d2);

    __m128 a3 = a2, b3 = b2;

    __m128 c3 = _mm_shuffle_ps(c2, c2, _MM_SHUFFLE(0, 1, 2, 3));

    __m128 d3 = _mm_shuffle_ps(d2, d2, _MM_SHUFFLE(0, 1, 2, 3));

    __m128 ad3Min = _mm_min_ps(a3, d3);

    __m128 ad3Max = _mm_max_ps(a3, d3);

    __m128 bc3Min = _mm_min_ps(b3, c3);

    __m128 bc3Max = _mm_max_ps(b3, c3);

    __m128 a4 = ad3Min;
    __m128 b4 = bc3Min;
    __m128 c4 = _mm_shuffle_ps(bc3Max, bc3Max, _MM_SHUFFLE(0, 1, 2, 3));
    __m128 d4 = _mm_shuffle_ps(ad3Max, ad3Max, _MM_SHUFFLE(0, 1, 2, 3));
    UpperHalfRightHalfBitonicSorter_SSE2(a4, b4, aOut, bOut);
    UpperHalfRightHalfBitonicSorter_SSE2(c4, d4, cOut, dOut);

}

This is verified using the 0/1 method described in Knuth.